题目内容
在直角坐标系xOy中,已知点P(
,1),直线l的参数方程为
(t为参数)若以O为极点,以Ox为极轴,选择相同的单位长度建立极坐标系,则曲线C的极坐标方程为ρ=
cos(θ-
)
(Ⅰ)求直线l的普通方程和曲线C的直角坐标方程;
(Ⅱ)设直线l与曲线C相交于A,B两点,求点P到A,B两点的距离之积.
| 1 |
| 2 |
|
| 2 |
| π |
| 4 |
(Ⅰ)求直线l的普通方程和曲线C的直角坐标方程;
(Ⅱ)设直线l与曲线C相交于A,B两点,求点P到A,B两点的距离之积.
考点:直线的参数方程,简单曲线的极坐标方程
专题:坐标系和参数方程
分析:(I)由直线l的参数方程
,由y=1+
t可得t=2(y-1)代入x=
+
t消去参数t即可得出;由曲线C的极坐标方程ρ=
cos(θ-
)展开为ρ=
(
cosθ+
sinθ),化为ρ2=ρcosθ+ρsinθ,利用
即可得出曲线C的直角坐标方程.
(II)把直线l的参数方程
代入圆的方程可得t2+
t-
=0,由于点P(
,1)在直线l上,可得|PA||PB|=|t1t2|.
|
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 2 |
| π |
| 4 |
| 2 |
| ||
| 2 |
| ||
| 2 |
|
(II)把直线l的参数方程
|
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
解答:
解:(I)由直线l的参数方程
,消去参数t,可得x-
y-
+
=0;
由曲线C的极坐标方程ρ=
cos(θ-
)展开为ρ=
(
cosθ+
sinθ),
化为ρ2=ρcosθ+ρsinθ,
∴曲线C的直角坐标方程为x2+y2=x+y,即(x-
)2+(y-
)2=
.
(II)把直线l的参数方程
代入圆的方程可得t2+
t-
=0,
∵点P(
,1)在直线l上,∴|PA||PB|=|t1t2|=
.
|
| 3 |
| 1 |
| 2 |
| 3 |
由曲线C的极坐标方程ρ=
| 2 |
| π |
| 4 |
| 2 |
| ||
| 2 |
| ||
| 2 |
化为ρ2=ρcosθ+ρsinθ,
∴曲线C的直角坐标方程为x2+y2=x+y,即(x-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(II)把直线l的参数方程
|
| 1 |
| 2 |
| 1 |
| 4 |
∵点P(
| 1 |
| 2 |
| 1 |
| 4 |
点评:本题考查了把参数方程极坐标方程化为直角坐标方程、直线参数方程的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
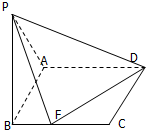 如图,已知平面PAB⊥平面ABCD,且四边形ABCD是矩形,AD:AB=3:2,△PAB为等边三角形,F是线段BC上的点且满足CF=2BF.
如图,已知平面PAB⊥平面ABCD,且四边形ABCD是矩形,AD:AB=3:2,△PAB为等边三角形,F是线段BC上的点且满足CF=2BF.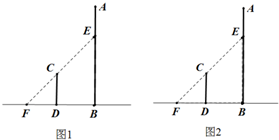 某公司为了公司周年庆典,现将公司门前广场进行装饰,广场上有一垂直于地面的墙面AB高为8+8
某公司为了公司周年庆典,现将公司门前广场进行装饰,广场上有一垂直于地面的墙面AB高为8+8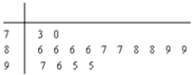 某电视台组织部分记者,用“10分制”随机调查某社区居民的幸福指数,现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福指数的得分(以小数点前的一位数字为茎,小数点后的一位数字为叶):
某电视台组织部分记者,用“10分制”随机调查某社区居民的幸福指数,现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福指数的得分(以小数点前的一位数字为茎,小数点后的一位数字为叶):
