题目内容
在三棱锥A-BCD中,AC⊥底面BCD,BD⊥DC,BD=DC,AC=a,∠ABC=30°,求点C到平面ABD的距离.
考点:点、线、面间的距离计算
专题:空间位置关系与距离
分析:AC⊥底面BCD,利用线面垂直的性质可得AC⊥BC.根据AC=a,∠ABC=30°,可得BC=
=
a.根据BD⊥DC,BD=DC,可得BD=CD=
,BD⊥AD.AD=
.设点C到平面ABD的距离为h.利用VA-BCD=VC-ABD,即可得出.
| AC |
| tan30° |
| 3 |
| ||
|
| AC2+CD2 |
解答:
解:如图所示,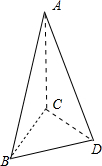
∵AC⊥底面BCD,∴AC⊥BC.
∵AC=a,∠ABC=30°,
∴BC=
=
a.
∵BD⊥DC,BD=DC,
∴BD=CD=
,BD⊥AD.
又AD=
=
=
a.
设点C到平面ABD的距离为h.
∵VA-BCD=VC-ABD,
∴
•S△BCD•AC=
•S△ABD•h.
∴
×(
)2•a=
•
•10a2•h,
∴h=
a.

∵AC⊥底面BCD,∴AC⊥BC.
∵AC=a,∠ABC=30°,
∴BC=
| AC |
| tan30° |
| 3 |
∵BD⊥DC,BD=DC,
∴BD=CD=
| ||
|
又AD=
| AC2+CD2 |
a2+(
|
| ||
| 2 |
设点C到平面ABD的距离为h.
∵VA-BCD=VC-ABD,
∴
| 1 |
| 3 |
| 1 |
| 3 |
∴
| 1 |
| 2 |
| ||
|
| 1 |
| 2 |
| ||
|
∴h=
| ||
| 5 |
点评:本题综合考查了线面垂直的性质定理、勾股定理、直角三角形的边角关系、三垂线定理、三角形的面积计算公式、三棱锥的体积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
已知(1+x)8=a0+a1x+a2x2+…+a8x8,则a1+a2+…+a8的值是( )
| A、28 |
| B、28-1 |
| C、26-1 |
| D、26 |
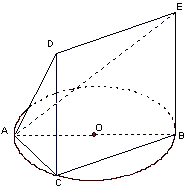 如图,△ABC内接于圆O,AB是圆O的直径,AB=2,BC=1,DC=
如图,△ABC内接于圆O,AB是圆O的直径,AB=2,BC=1,DC=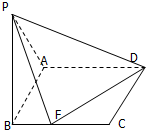 如图,已知平面PAB⊥平面ABCD,且四边形ABCD是矩形,AD:AB=3:2,△PAB为等边三角形,F是线段BC上的点且满足CF=2BF.
如图,已知平面PAB⊥平面ABCD,且四边形ABCD是矩形,AD:AB=3:2,△PAB为等边三角形,F是线段BC上的点且满足CF=2BF.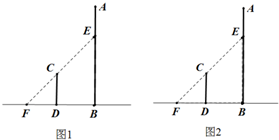 某公司为了公司周年庆典,现将公司门前广场进行装饰,广场上有一垂直于地面的墙面AB高为8+8
某公司为了公司周年庆典,现将公司门前广场进行装饰,广场上有一垂直于地面的墙面AB高为8+8