题目内容
10.已知函数f(x)=x3+$\frac{5}{2}$x2+ax+b(a,b为常数),其图象是曲线C.(1)当a=-2时,求函数f(x)的单调减区间;
(2)设函数f(x)的导函数为f′(x),若存在唯一的实数x0,使得f(x0)=x0与f′(x0)=0同时成立,求实数b的取值范围.
分析 (1)先求原函数的导数,根据f′(x)<0求得的区间是单调减区间,即可;
(2)由于存在唯一的实数x0,使得f(x0)=x0与f′(x0)=0同时成立,则$\left\{\begin{array}{l}{{x}^{3}+\frac{5}{2}{x}^{2}+(a-1)x+b=0}\\{3{x}^{2}+5x+a=0}\end{array}\right.$存在唯一的实数根x0,即b=2x3+$\frac{5}{2}$x2+x存在唯一的实数根x0,就把问题转化为求函数最值问题
解答 解:(1)当a=-2时,函数f(x)=x3+$\frac{5}{2}$x2-2x+b
则f′(x)=3x2+5x-2=(3x-1)(x+2)
令f′(x)<0,解得-2<x<$\frac{1}{3}$,
所以f(x)的单调递减区间为(-2,$\frac{1}{3}$);
(2)函数f(x)的导函数为由于存在唯一的实数x0,使得f(x0)=x0与f′(x0)=0同时成立,
则$\left\{\begin{array}{l}{{x}^{3}+\frac{5}{2}{x}^{2}+(a-1)x+b=0}\\{3{x}^{2}+5x+a=0}\end{array}\right.$即x3+$\frac{5}{2}$x2+(-3x2-5x-1)x+b=0存在唯一的实数根x0,
故b=2x3+$\frac{5}{2}$x2+x存在唯一的实数根x0,
令y=2x3+$\frac{5}{2}$x2+x,则y′=6x2+5x+1=(2x+1)(3x+1)=0,故x=-$\frac{1}{2}$或x=-$\frac{1}{3}$,
则函数y=2x3+$\frac{5}{2}$x2+x在(-∞,-$\frac{1}{2}$),(-$\frac{1}{3}$,+∞)上是增函数,在(-$\frac{1}{2}$,-$\frac{1}{3}$)上是减函数,
由于x=-$\frac{1}{2}$时,y=-$\frac{1}{8}$;x=-$\frac{1}{3}$时,y=-$\frac{7}{54}$;
故实数b的取值范围为:(-∞,-$\frac{7}{54}$)∪(-$\frac{1}{8}$,+∞);
点评 本题以函数为载体,考查导数知识的运用,考查函数的单调性,同时还考查了方程根的问题,一般要转化为函数的最值来解决.

| A. | bf(a)≤af(b) | B. | af(b)≤bf(a) | C. | bf(a)≤f(a) | D. | af(a)≤f(b) |
 如图,四棱锥P-ABCD中,PB⊥底面ABCD.底面ABCD为直角梯形,∠ABC=90°,AD∥BC,BC=2,AB=AD=PB=1,点E为棱PA的中点.
如图,四棱锥P-ABCD中,PB⊥底面ABCD.底面ABCD为直角梯形,∠ABC=90°,AD∥BC,BC=2,AB=AD=PB=1,点E为棱PA的中点.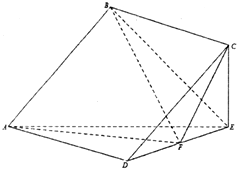 在几何体ABCDE中,四边形ABCD是正方形,CE⊥平面ADE且CE=EF=2,F是线段DE的中点.
在几何体ABCDE中,四边形ABCD是正方形,CE⊥平面ADE且CE=EF=2,F是线段DE的中点.