题目内容
16.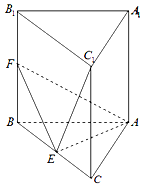 如图,在三棱柱ABC-A1B1C1中,AB、AC、AA1三条棱两两互相垂直,且AB=AC=AA1=2,E、F分别是BC、BB1的中点.
如图,在三棱柱ABC-A1B1C1中,AB、AC、AA1三条棱两两互相垂直,且AB=AC=AA1=2,E、F分别是BC、BB1的中点.(Ⅰ)求证:C1E⊥平面AEF;
(Ⅱ)求F到平面AEC1的距离.
分析 (1)根据勾股定理证明EF⊥EC1,AE⊥EC1,再根据线面垂直定理可以证明.
(2)方法1:设求F到平面AEC1的距离为d,由等体积法${V}_{F-AE{C}_{1}}$=${V}_{{C}_{1}-FAE}$,即可求出d,
方法2,判断出EF即为点F到面AEC1的距离,即可求出.
解答  解:(1)连接FC1、AC1,由已知可得
解:(1)连接FC1、AC1,由已知可得
$BC=2\sqrt{2},C{C_1}=2,{C_1}E=\sqrt{6},AE=\sqrt{2},A{C_1}=2\sqrt{2},EF=\sqrt{3},F{C_1}=3$,
∴$F{C_1}^2=E{F^2}+E{C_1}^2,A{C_1}^2=A{E^2}+E{C_1}^2$,
∴EF⊥EC1,AE⊥EC1,
又∵EF、AE?面AEF,EF∩AE=E,
故C1E⊥平面AEF
(2)方法1:由已知得$AF=\sqrt{5}$,
∴AF2=EF2+AE2,
∴EF⊥AE,
由(1)知C1E⊥平面AEF,则C1E为三棱锥C1-AEF的高,
设求F到平面AEC1的距离为d,由等体积法${V}_{F-AE{C}_{1}}$=${V}_{{C}_{1}-FAE}$,
∴$\frac{1}{3}×({\frac{1}{2}×AE×{C_1}E})×d=\frac{1}{3}×({\frac{1}{2}×AE×EF})×{C_1}E$,
∴$\frac{1}{3}×({\frac{1}{2}×\sqrt{2}×\sqrt{6}})×d=\frac{1}{3}×({\frac{1}{2}×\sqrt{2}×\sqrt{3}})×\sqrt{6}$,
∴$d=\sqrt{3}$,即F到平面AEC1的距离为$\sqrt{3}$.
方法2:${C_1}E=\sqrt{6},AE=\sqrt{2},AF=\sqrt{5},EF=\sqrt{3},F{C_1}=3$,
∴$E{F^2}+A{E^2}={({\sqrt{3}})^2}+{({\sqrt{2}})^2}={({\sqrt{5}})^2}=A{E^2}$,
∴EF⊥AE,
∴$E{F^2}+{C_1}{E^2}═{({\sqrt{3}})^2}+{({\sqrt{6}})^2}={3^2}={C_1}{F^2}∴EF⊥{C_1}E$,
又∵C1E、AE?面AEF,C1E∩AE=E,
∴EF⊥面AEC1,
∴EF即为点F到面AEC1的距离,$EF=\sqrt{3}$,
即F到平面AEC1的距离为$\sqrt{3}$.
点评 本题考查直线与平面垂直的判定,考查了点到直线的距离,考查空间想象能力和思维能力,是中档题.

| A. | (-2,3) | B. | (-4,2) | C. | (-4,3) | D. | (2,3) |
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 非充分非必要条件 |
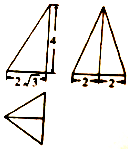 若一个几何体的三视图如图所示,则这个几何体的外接球的表面积为( )
若一个几何体的三视图如图所示,则这个几何体的外接球的表面积为( )| A. | 34π | B. | $\frac{80π}{3}$ | C. | $\frac{91}{3}π$ | D. | 114π |
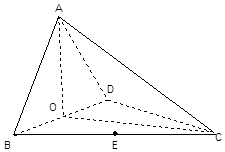 如图,四面体ABCD中,O、E分别是BD、BC的中点,底面BCD是正三角形,AC=BD=2,AB=AD=$\sqrt{2}$.
如图,四面体ABCD中,O、E分别是BD、BC的中点,底面BCD是正三角形,AC=BD=2,AB=AD=$\sqrt{2}$.