题目内容
2.已知函数f(x)=|2x-1|+|x-2a|.(1)当a=1时,求f(x)≤3的解集;
(2)当x∈[1,2]时,f(x)≤3恒成立,求实数a的取值范围.
分析 (1)当a=1时,求得函数的解析式,分类当x>2时,3x-3≤3,则x≤2,不等式无解;当$\frac{1}{2}$≤x≤2时,x+1≤3,则x≤2,当x<$\frac{1}{2}$时,3-3x≤3,则x≥0,即可求得f(x)≤3的解集;
(2)由|x-2a|≤3-|2x-1|,由x∈[1,2],即|x-2a|≤4-2x,2x-4≤x-2a≤4-2x,$\frac{3x-4}{2}$≤a≤$\frac{4-x}{2}$,对x∈[1,2]恒成立,当1≤x≤2时,3x-4的最大值2,4-x的最小值为3,即可求得实数a的取值范围.
解答 解:(1)由题意可知:当a=1时,原不等式可化为:f(x)=|2x-1|+|x-2a|=$\left\{\begin{array}{l}{3-3x}&{x≤\frac{1}{2}}\\{1+x}&{\frac{1}{2}<x<2}\\{3x-3}&{x≥2}\end{array}\right.$,
依题意,当x>2时,3x-3≤3,则x≤2,不等式无解;当$\frac{1}{2}$≤x≤2时,x+1≤3,则x≤2,
∴$\frac{1}{2}$≤x≤2;
当x<$\frac{1}{2}$时,3-3x≤3,则x≥0,
∴0≤x<$\frac{1}{2}$;
综上可知:原不等式的解集为:{x丨0≤x≤2}
(2)原不等式可化为:|x-2a|≤3-|2x-1|,由x∈[1,2],
∴|x-2a|≤4-2x,即:2x-4≤x-2a≤4-2x,
∴$\frac{3x-4}{2}$≤a≤$\frac{4-x}{2}$,对x∈[1,2]恒成立,
当1≤x≤2时,3x-4的最大值2,4-x的最小值为3,
∴实数a的取值范围:a=1.
实数a的取值范围{1}.
点评 本题考查分段函数的解集,考查含绝对值函数的应用,考查分类讨论思想,不等式的解法,考查计算能力,属于中档题.

| A. | $\frac{4}{3}π$ | B. | $\frac{7}{3}π$ | C. | 2π | D. | $\frac{7}{2}π$ |
| A. | $(1,\sqrt{3)}$ | B. | $({1,\frac{{\sqrt{10}}}{2}}]$ | C. | (1,2) | D. | (1,2] |
| A. | -1 | B. | $\frac{1}{2}$ | C. | $-\frac{1}{2}$ | D. | 1 |
| A. | $-\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | $-\frac{5}{2}$ | D. | $\frac{5}{2}$ |
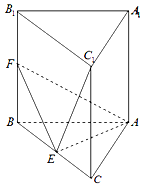 如图,在三棱柱ABC-A1B1C1中,AB、AC、AA1三条棱两两互相垂直,且AB=AC=AA1=2,E、F分别是BC、BB1的中点.
如图,在三棱柱ABC-A1B1C1中,AB、AC、AA1三条棱两两互相垂直,且AB=AC=AA1=2,E、F分别是BC、BB1的中点.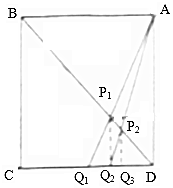 如图,已知ABCD是边长为1的正方形,Q1为CD的中点,Pi(i=1,2…,n)为AQi与BD的交点,过Pi作CD的垂线,垂足为Qi+1,则$\sum_{i=1}^{10}$S${\;}_{△D{Q_i}{P_i}}$=$\frac{5}{24}$.
如图,已知ABCD是边长为1的正方形,Q1为CD的中点,Pi(i=1,2…,n)为AQi与BD的交点,过Pi作CD的垂线,垂足为Qi+1,则$\sum_{i=1}^{10}$S${\;}_{△D{Q_i}{P_i}}$=$\frac{5}{24}$.