题目内容
11．已知a、b 是实数，则“a＞b”是“a2＞b2”的（ ）| A． | 充分非必要条件 | B． | 必要非充分条件 | ||
| C． | 充要条件 | D． | 非充分非必要条件 |
分析 根据充分必要条件的定义判断即可．
解答 解：由a＞b推不出a2＞b2，比如a=0，b=-2，不是充分条件，
由a2＞b2推不出a＞b，比如a=-2，b=0，不是必要条件，
故选：D．
点评 本题考查了充分必要条件，考查不等式问题，是一道基础题．
练习册系列答案
名校课堂系列答案
相关题目
1．已知$cos\frac{4π}{5}cos\frac{7π}{15}+sin\frac{4π}{5}sin\frac{7π}{15}$=$\frac{2}{3}+cos（\frac{π}{2}+x）cosx$则sin2x等于（ ）
| A． | $\frac{1}{3}$ | B． | -$\frac{1}{3}$ | C． | $\frac{1}{12}$ | D． | -$\frac{1}{12}$ |
19．已知{an}是等差数列，a3+a11=40，则a6-a7+a8等于（ ）
| A． | 20 | B． | 48 | C． | 60 | D． | 72 |
6．已知函数f（x）=2sinxcosx+cos2x，则下列说法正确的是（ ）
| A． | f（x）的图象向右平移$\frac{π}{4}$个单位长度后得到$g（x）=\sqrt{2}sin（2x+\frac{π}{4}）$的图象 | |
| B． | 若f（x1）=f（x2），则x1-x2=kπ，k∈Z | |
| C． | f（x）的图象关于直线$x=\frac{5}{8}π$对称 | |
| D． | f（x）的图象关于点$（-\frac{3}{8}π，0）$对称 |
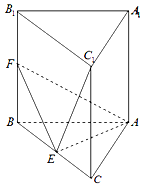如图，在三棱柱ABC-A1B1C1中，AB、AC、AA1三条棱两两互相垂直，且AB=AC=AA1=2，E、F分别是BC、BB1的中点．
1．直线x+2y-1=0在y轴上的截距为（ ）
| A． | -1 | B． | $\frac{1}{2}$ | C． | $-\frac{1}{2}$ | D． | 1 |