题目内容
1.设命题p:实数x满足x2-4ax+3a2<0(a>0),命题q:实数x满足$\frac{x-3}{x-2}≤0$.(1)若命题p的解集为P,命题q的解集为Q,当a=1时,求P∩Q;
(2)若¬p是¬q的充分不必要条件,求实数a的取值范围.
分析 (1)分别求出P,Q,求出P,Q的交集即可;
(2)分别求出¬p,¬q,根据¬p是¬q的充分不必要条件,求出a的范围即可.
解答 解:(1)若a=1,由x2-4x+3<0得:1<x<3,∴P=(1,3)--------------(2分)
由$\frac{x-3}{x-2}$≤0得:2<x≤3;∴Q=(2,3]-------------------------------------------------------------(4分)
∴P∩Q=(2,3)---------------------------------------(5分)
(2)¬q为:实数x满足x≤2,或x>3;
¬p为:实数x满足x2-4ax+3a2≥0,并解x2-4ax+3a2≥0得x≤a,或x≥3a-----------------(7分)
¬p是¬q的充分不必要条件,所以a应满足:a≤2,且3a>3,解得1<a≤2---------------(9分)
∴a的取值范围为:(1,2]----------------------------------(10分)
点评 本题考查了充分必要条件,考查解不等式问题以及集合的运算,是一道中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
12.已知a>0,函数f(x)=x2+alnx-ax在(0,+∞)上是增函数,则a的最大值为( )
| A. | 2 | B. | $2\sqrt{2}$ | C. | 4 | D. | 8 |
9.若a=log0.60.3,b=0.60.3,则( )
| A. | a>1>b | B. | a>b>1 | C. | b>a>1 | D. | b>1>a |
10.在正项等比数列{an}中,a3=2,a4=8a7,则a9=( )
| A. | $\frac{1}{256}$ | B. | $\frac{1}{128}$ | C. | $\frac{1}{64}$ | D. | $\frac{1}{32}$ |
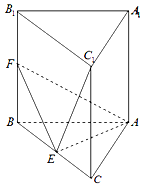 如图,在三棱柱ABC-A1B1C1中,AB、AC、AA1三条棱两两互相垂直,且AB=AC=AA1=2,E、F分别是BC、BB1的中点.
如图,在三棱柱ABC-A1B1C1中,AB、AC、AA1三条棱两两互相垂直,且AB=AC=AA1=2,E、F分别是BC、BB1的中点.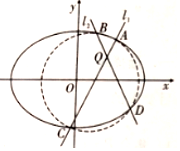 已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>1})$中,a=$\sqrt{2}$b,且椭圆E上任一点到点$P({-\frac{1}{2},0})$的最小距离为$\frac{{\sqrt{7}}}{2}$.
已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>1})$中,a=$\sqrt{2}$b,且椭圆E上任一点到点$P({-\frac{1}{2},0})$的最小距离为$\frac{{\sqrt{7}}}{2}$.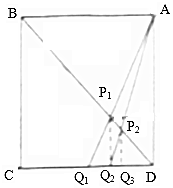 如图,已知ABCD是边长为1的正方形,Q1为CD的中点,Pi(i=1,2…,n)为AQi与BD的交点,过Pi作CD的垂线,垂足为Qi+1,则$\sum_{i=1}^{10}$S${\;}_{△D{Q_i}{P_i}}$=$\frac{5}{24}$.
如图,已知ABCD是边长为1的正方形,Q1为CD的中点,Pi(i=1,2…,n)为AQi与BD的交点,过Pi作CD的垂线,垂足为Qi+1,则$\sum_{i=1}^{10}$S${\;}_{△D{Q_i}{P_i}}$=$\frac{5}{24}$.