题目内容
有10只不同的试验产品,其中有4只次品,6只正品,现每次取一只测试,直到测出1只次品为止,求第一只次品正好在第五次测试时被发现的不同情形有 种.
考点:排列、组合及简单计数问题
专题:概率与统计
分析:第一只次品正好在第五次测试时被发现的不同情形为:前4次检测时测出的都是正品,第5次检测时测出的是次品,由此能求出结果.
解答:
解:第一只次品正好在第五次测试时被发现的不同情形为:
前4次检测时测出的都是正品,第5次检测时测出的是次品,
故第一只次品正好在第五次测试时被发现的不同情形有:
=1440.
故答案为:1440.
前4次检测时测出的都是正品,第5次检测时测出的是次品,
故第一只次品正好在第五次测试时被发现的不同情形有:
| C | 4 6 |
| C | 4 4 |
| C | 1 4 |
故答案为:1440.
点评:本题考查排列组合的计数问题的应用,解题时要认真审题,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在某次数学测验中,记座号为n(n=1,2,3,4)的同学成绩为f(n),若f(n)∈{70,85,88,90,98,100},且满足f(1)<f(2)≤f(3)<f(4),则这四位同学考试成绩的所有可能有( )种.
| A、15 | B、20 | C、30 | D、35 |
下列结论正确的是( )
| A、若y=cosx,则y′=sinx | ||||
B、若y=sin
| ||||
C、若y=lnx,则y′=
| ||||
| D、若y=2x,则y′=x2x-1 |
如图所示,甲 乙 丙是三个立体图形的三视图,则甲乙丙对应的标号正确的是( )

| A、④③② | B、②①③ |
| C、①②③ | D、③②④ |
定义A㊣B、B㊣C、C㊣D、D㊣A的运算分别对应图中的(1)、(2)、(3)、(4).则图中的甲、乙的运算式可以表示为:( )
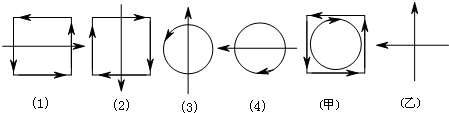

| A、B㊣D、C㊣A |
| B、B㊣D、A㊣C |
| C、D㊣B、C㊣A |
| D、D㊣B、A㊣C |