题目内容
已知函数f(x)的定义域中R,等式f(1-x)=f(1+x)与f(x-1)=f(x-3)对任意的实数x都成立,当x∈[1,2]时,f(x)=x2,那么f(x)的单调减区间是(注:以下各选项中k∈z)( )
| A、[2k,2k+1] |
| B、[2k-1,2k] |
| C、[2k,2k+2] |
| D、[2k-2,2k] |
考点:抽象函数及其应用,函数单调性的判断与证明
专题:函数的性质及应用
分析:根据条件先判断出函数f(x)的对称轴,再判断出函数为周期函数,根据函数的单调性即可求出答案.
解答:
解:∵f(1-x)=f(1+x),
∴函数f(x)的对称轴为x=1,
∵f(x-1)=f(x-3),
令x=x+3,
得f(x+2)=f(x),
∴函数f(x)为以2周期的周期函数,
∵x∈[1,2]时,f(x)=x2,
∴函数f(x)在区间[1,2]上单调递增.
∴函数f(x)在区间[0,1]上单调递减.
∴f(x)的单调减区间是[2k,2k+1](k∈Z).
故选:A
∴函数f(x)的对称轴为x=1,
∵f(x-1)=f(x-3),
令x=x+3,
得f(x+2)=f(x),
∴函数f(x)为以2周期的周期函数,
∵x∈[1,2]时,f(x)=x2,
∴函数f(x)在区间[1,2]上单调递增.
∴函数f(x)在区间[0,1]上单调递减.
∴f(x)的单调减区间是[2k,2k+1](k∈Z).
故选:A
点评:本题主要考查了函数的奇偶性,对称性,单调性,周期性,关键求出是函数为周期函数,属于中档题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
已知函数f(x)=cos2x-tcosx在x∈[
,
]上为单调递增函数,则实数t的取值范围是( )
| π |
| 6 |
| π |
| 3 |
A、[2
| ||
B、[
| ||
| C、(-∞,2] | ||
| D、(-∞,1] |
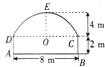 如图所示的图形为一隧道的截面,其中ABCD是矩形,CED是抛物线的一段,在工程的设计中,要注意开凿隧道所需挖掘的土石方量,这就需要计算这个截面的面积,试根据图中所给出的数据计算这个截面的面积.
如图所示的图形为一隧道的截面,其中ABCD是矩形,CED是抛物线的一段,在工程的设计中,要注意开凿隧道所需挖掘的土石方量,这就需要计算这个截面的面积,试根据图中所给出的数据计算这个截面的面积.