题目内容
已知函数f(x)是奇函数,且当x>0时,f(x)=x2+
,则f(-1)=( )
| 1 |
| x |
| A、-2 | B、0 | C、1 | D、2 |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:由奇函数定义得,f(-1)=-f(1),根据x>0的解析式,求出f(1),从而得到f(-1).
解答:
解:∵f(x)是定义在R上的奇函数,
∴f(-x)=-f(x),f(-1)=-f(1),
又当x>0时,f(x)=x2+
,
∴f(1)=12+1=2,∴f(-1)=-2,
故选:A.
∴f(-x)=-f(x),f(-1)=-f(1),
又当x>0时,f(x)=x2+
| 1 |
| x |
∴f(1)=12+1=2,∴f(-1)=-2,
故选:A.
点评:本题考查函数的奇偶性及运用,主要是奇函数的定义及运用,解题时要注意自变量的范围,正确应用解析式求函数值,本题属于基础题.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
下列说法正确的是( )
| A、方向相同或相反的向量是平行向量 | ||
B、零向量是
| ||
| C、长度相等的向量叫做相等向量 | ||
| D、共线向量是在一条直线上的向量 |
在等差数列{an}中,a3=5则{an}的前5项和S5=( )
| A、7 | B、15 | C、25 | D、20 |
| ∫ | 2 -2 |
| A、0 | B、1 | C、8 | D、16 |
已知实数x,y满足ax<ay(a>1),则下列关系式恒成立的是( )
A、
| ||||
| B、ln(x2+1)<ln(y2+1) | ||||
| C、sinx<siny | ||||
| D、x3<y3 |
已知cosθ=-
,θ∈(
,π),则tanθ等于( )
| 3 |
| 5 |
| π |
| 2 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
经过两直线x+3y-10=0和3x-y=0的交点,且和原点相距为1的直线的条数为( )
| A、0 | B、1 | C、2 | D、3 |
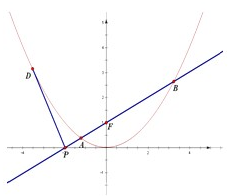 抛物线C:x2=4y,直线AB过抛物线C的焦点F,交x轴于点P.
抛物线C:x2=4y,直线AB过抛物线C的焦点F,交x轴于点P.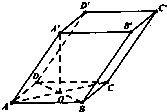 如图四棱柱ABCD-A′B′C′D′的底面是正方形,O是底面的中心,A′O=1,AB=AA′=A′D=A′B=
如图四棱柱ABCD-A′B′C′D′的底面是正方形,O是底面的中心,A′O=1,AB=AA′=A′D=A′B=