题目内容
6.函数$f(x)=\frac{{\root{3}{3x+5}}}{{a{x^2}+4ax+3}}$的定义域为R,则实数a的取值范围是( )| A. | (-∞,+∞) | B. | $(0,\frac{3}{4})$ | C. | $(\frac{3}{4},+∞)$ | D. | $[0,\frac{3}{4})$ |
分析 由函数$f(x)=\frac{{\root{3}{3x+5}}}{{a{x^2}+4ax+3}}$的定义域为R,得对任意实数x,ax2+4ax+3≠0,然后分a=0和a≠0讨论,当a≠0时,由△=16a2-12a<0求得a的取值范围.
解答 解:由函数$f(x)=\frac{{\root{3}{3x+5}}}{{a{x^2}+4ax+3}}$的定义域为R,得
对任意实数x,ax2+4ax+3≠0,
当a=0时,ax2+4ax+3=3≠0成立;
当a≠0时,则△=16a2-12a<0,即0<a<$\frac{3}{4}$.
综上,实数a的取值范围是[0,$\frac{3}{4}$).
故选:D.
点评 本题考查函数的定义域及其求法,考查了分类讨论的数学思想方法,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.已知$cos({60°}+α)=\frac{1}{3}$,且-180°<α<-90°,则cos(30°-α)的值为( )
| A. | $-\frac{{2\sqrt{2}}}{3}$ | B. | $\frac{{2\sqrt{2}}}{3}$ | C. | $-\frac{{\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{2}}}{3}$ |
15.下列语句:
①{0}∈N;
②x2+y2=0;
③x2>x;
④{x|x2+1=0}.
其中是命题的个数是( )
①{0}∈N;
②x2+y2=0;
③x2>x;
④{x|x2+1=0}.
其中是命题的个数是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
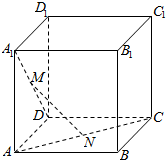 如图,在棱长为a的正方体ABCD-A1B1C1D1中,M为A1D中点,N为AC中点.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,M为A1D中点,N为AC中点.