题目内容
1.等比数列{an}前n项和为Sn=a+($\frac{1}{3}$)n,n∈N*,则$\lim_{n→∞}$(a1+a3+a5+…+a2n-1)=-$\frac{3}{4}$.分析 先求出数列的前3项,由等比数列的性质求出首项和公比,由此能求出$\lim_{n→∞}$(a1+a3+a5+…+a2n-1).
解答 解:∵等比数列{an}前n项和为Sn=a+($\frac{1}{3}$)n,n∈N*,
∴a1=S1=a+$\frac{1}{3}$,
a2=S2-S1=[a+($\frac{1}{3}$)2]-(a+$\frac{1}{3}$)=-$\frac{2}{9}$,
a3=S3-S2=[a+($\frac{1}{3}$)3]-[a+($\frac{1}{3}$)2]=-$\frac{2}{27}$,
∴(-$\frac{2}{9}$)2=(a+$\frac{1}{3}$)(-$\frac{2}{27}$),解得a=-1,${a}_{1}=-\frac{2}{3}$,q=$\frac{-\frac{2}{9}}{-\frac{2}{3}}$=$\frac{1}{3}$,
∴${a}_{n}=(-\frac{2}{3})•(\frac{1}{3})^{n-1}$=(-2)$•\frac{1}{{3}^{n}}$.
∴$\lim_{n→∞}$(a1+a3+a5+…+a2n-1)=$\lim_{n→∞}$($\frac{-\frac{2}{3}(1-\frac{1}{{9}^{n}})}{1-\frac{1}{9}}$)=$\frac{-\frac{2}{3}}{1-\frac{1}{9}}$=-$\frac{3}{4}$.
故答案为:-$\frac{3}{4}$.
点评 本题考查数列的前2n项中奇数项和的极限的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
相关题目
11.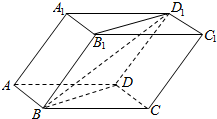 已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则异面直线BD1与AA1所成的角的余弦值为( )
已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则异面直线BD1与AA1所成的角的余弦值为( )
 已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则异面直线BD1与AA1所成的角的余弦值为( )
已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则异面直线BD1与AA1所成的角的余弦值为( )| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{13}}{4}$ | C. | $\frac{\sqrt{39}}{13}$ | D. | $\frac{3}{4}$ |
6.函数$f(x)=\frac{{\root{3}{3x+5}}}{{a{x^2}+4ax+3}}$的定义域为R,则实数a的取值范围是( )
| A. | (-∞,+∞) | B. | $(0,\frac{3}{4})$ | C. | $(\frac{3}{4},+∞)$ | D. | $[0,\frac{3}{4})$ |
11.已知a,b∈R,下列结论成立的是( )
| A. | 若a<b,则ac<bc | B. | 若a<b,c<d,则ac<bd | ||
| C. | 若a<b<0,则$\frac{1}{a}$>$\frac{1}{b}$ | D. | 若a<b,则an<bn(n∈N*,n≥2) |