题目内容
14.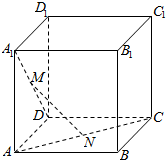 如图,在棱长为a的正方体ABCD-A1B1C1D1中,M为A1D中点,N为AC中点.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,M为A1D中点,N为AC中点.(1)求异面直线MN和AB所成的角;
(2)求证:MN⊥AB1.
分析 (1)以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出异面直线MN和AB所成的角的大小.
(2)分别求出$\overrightarrow{MN}$,$\overrightarrow{A{B}_{1}}$,利用向量法能证明MN⊥AB1.
解答  解:(1)以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
解:(1)以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
由题意得M($\frac{a}{2}$,0,$\frac{a}{2}$),N($\frac{a}{2},\frac{a}{2}$,0),A(a,0,0),B(a,a,0),
$\overrightarrow{MN}$=(0,$\frac{a}{2}$,-$\frac{a}{2}$),$\overrightarrow{AB}$=(0,a,0),
设MN和AB所成的角为θ,
则cosθ=|$\frac{\overrightarrow{MN}•\overrightarrow{AB}}{|\overrightarrow{MN}|•|\overrightarrow{AB}|}$|=|$\frac{\frac{{a}^{2}}{2}}{\frac{\sqrt{2}}{2}{a}^{2}}$|=$\frac{\sqrt{2}}{2}$,
∴θ=45°,
∴异面直线MN和AB所成的角为45°.
证明:(2)$\overrightarrow{MN}$=(0,$\frac{a}{2}$,-$\frac{a}{2}$),B1(a,a,a),$\overrightarrow{A{B}_{1}}$=(0,a,a),
∴$\overrightarrow{MN}•\overrightarrow{A{B}_{1}}$=0+$\frac{{a}^{2}}{2}-\frac{{a}^{2}}{2}$=0,
∴MN⊥AB1.
点评 本题考查异面直线所成角的求法,考查异面垂直的证明,是基础题,解题时要认真审题,注意向量法的合理运用.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
| A. | 自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系 | |
| B. | 在线性回归分析中,相关系数r的值越大,变量间的相关性越强 | |
| C. | 在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高 | |
| D. | 在回归分析中,R2为0.98的模型比R2为0.80的模型拟合的效果好 |
| A. | (-∞,+∞) | B. | $(0,\frac{3}{4})$ | C. | $(\frac{3}{4},+∞)$ | D. | $[0,\frac{3}{4})$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
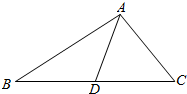 在△ABC中,D是BC中点,已知∠BAD+∠C=90°.
在△ABC中,D是BC中点,已知∠BAD+∠C=90°.