题目内容
2.如果z是3+4i的共轭复数,则z对应的向量$\overrightarrow{OA}$的模是( )| A. | 1 | B. | $\sqrt{7}$ | C. | $\sqrt{13}$ | D. | 5 |
分析 由题意求得z,进一步得到向量$\overrightarrow{OA}$的坐标,代入向量模的公式计算.
解答 解:由题意,z=3-4i,
∴z对应的向量$\overrightarrow{OA}$的坐标为(3,-4),其模为$\sqrt{{3}^{2}+(-4)^{2}}=5$.
故选:D.
点评 本题考查复数的代数表示法及其几何意义,考查向量模的求法,是基础题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
19.某中学拟在高一下学期开设游泳选修课,为了了解高一学生喜欢游泳是否与性别有关,现从高一学生中抽取100人做调查,得到如下2×2列联表:
已知在这100人中随机抽取一人抽到喜欢游泳的学生的概率为$\frac{3}{5}$.
(Ⅰ)请将上述列联表补充完整,并判断是否有99.9%的把握认为喜欢游泳与性别有关?并说明你的理由;
(Ⅱ)针对问卷调查的100名学生,学校决定从喜欢游泳的人中按分层抽样的方法随机抽取6人成立游泳科普知识宣传组,并在这6人中任选两人作为宣传组的组长,求这两人中至少有一名女生的概率.
参考公式:${Χ^2}=\frac{{n{{({n_{11}}{n_{22}}-{n_{12}}{n_{21}})}^2}}}{{{n_{1+}}{n_{2+}}{n_{+1}}{n_{+2}}}}$,其中n=n11+n12+n21+n22.
参考数据:
| 喜欢游泳 | 不喜欢游泳 | 合计 | |
| 男生 | 40 | 10 | 50 |
| 女生 | 20 | 30 | 50 |
| 合计 | 60 | 40 | 100 |
(Ⅰ)请将上述列联表补充完整,并判断是否有99.9%的把握认为喜欢游泳与性别有关?并说明你的理由;
(Ⅱ)针对问卷调查的100名学生,学校决定从喜欢游泳的人中按分层抽样的方法随机抽取6人成立游泳科普知识宣传组,并在这6人中任选两人作为宣传组的组长,求这两人中至少有一名女生的概率.
参考公式:${Χ^2}=\frac{{n{{({n_{11}}{n_{22}}-{n_{12}}{n_{21}})}^2}}}{{{n_{1+}}{n_{2+}}{n_{+1}}{n_{+2}}}}$,其中n=n11+n12+n21+n22.
参考数据:
| P(Χ2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
10.设f(x)是定义在R上的函数,其导函数为f′(x),若f(x)+f′(x)>1,f(0)=2017,则不等式exf(x)>ex+2016(其中e为自然对数的底数)的解集为( )
| A. | (-∞,0)∪(0,+∞) | B. | (0,+∞) | C. | (2016,+∞) | D. | (-∞,0)∪(2016,+∞) |
7.已知一个几何体的三视图如图所示,则该几何体的体积是( )
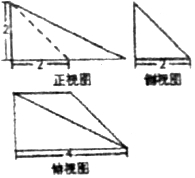

| A. | 2 | B. | 4 | C. | 6 | D. | 1 |
12.在△ABC中,“sinA=sinB”是“A=B”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |