题目内容
10.设f(x)是定义在R上的函数,其导函数为f′(x),若f(x)+f′(x)>1,f(0)=2017,则不等式exf(x)>ex+2016(其中e为自然对数的底数)的解集为( )| A. | (-∞,0)∪(0,+∞) | B. | (0,+∞) | C. | (2016,+∞) | D. | (-∞,0)∪(2016,+∞) |
分析 构造函数g(x)=exf(x)-ex,则可判断g′(x)>0,故g(x)为增函数,结合g(0)=2016即可得出答案.
解答 解:设g(x)=exf(x)-ex,则g′(x)=exf(x)+exf′(x)-ex=ex[f(x)+f′(x)-1],
∵f(x)+f′(x)>1,ex>0,
∴g′(x)=ex[f(x)+f′(x)-1]>0,
∴g(x)是R上的增函数,
又g(0)=f(0)-1=2016,
∴g(x)>2016的解集为(0,+∞),
即不等式exf(x)>ex+2016的解集为(0,+∞).
故选B.
点评 本题考查了导数与函数单调性的关系,构造函数g(x)是解题的关键,属于中档题.

练习册系列答案
相关题目
5.四个人围坐在一张圆桌旁,每个人面前放着完全相同的硬币,所有人同时翻转自己的硬币.若硬币正面朝上,则这个人站起来; 若硬币正面朝下,则这个人继续坐着.那么,没有相邻的两个人站起来的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{7}{16}$ | C. | $\frac{1}{2}$ | D. | $\frac{9}{16}$ |
15.已知函数$f(x)=\left\{{\begin{array}{l}{{x^2}+(4a-3)x+3a,x<0}\\{{{log}_a}(x+1)+1,x≥0}\end{array}}\right.(a>0且a≠1)$在R上单调递减,且关于x的方程$|f(x)|=2-\frac{x}{3}$恰有两个不相等的实数解,则a的取值范围是( )
| A. | (0,$\frac{2}{3}$] | B. | [$\frac{2}{3}$,$\frac{3}{4}$] | C. | [$\frac{1}{3}$,$\frac{2}{3}$] | D. | [$\frac{1}{3}$,$\frac{2}{3}$) |
2.如果z是3+4i的共轭复数,则z对应的向量$\overrightarrow{OA}$的模是( )
| A. | 1 | B. | $\sqrt{7}$ | C. | $\sqrt{13}$ | D. | 5 |
20.下列各组函数表示相等函数的是( )
| A. | $f(x)={({\sqrt{x}})^2}$和$g(x)=\sqrt{x^2}$ | B. | $f(x)={({\root{3}{x+1}})^3}$和$g(x)=\root{3}{{{{({x+1})}^3}}}$ | ||
| C. | f(x)=2lgx和g(x)=lg x2 | D. | f(x)=ln x-ln(x-1)和$g(x)=ln\frac{x}{x-1}$ |
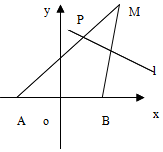 已知A点坐标为$(-2\sqrt{3},0)$,B点坐标为$(2\sqrt{3},0)$,且动点M到A点的距离是8,线段MB的垂直平分线l交线段MA于点P.
已知A点坐标为$(-2\sqrt{3},0)$,B点坐标为$(2\sqrt{3},0)$,且动点M到A点的距离是8,线段MB的垂直平分线l交线段MA于点P.