题目内容
14.已知椭圆16x2+25y2=400(Ⅰ)求椭圆的长轴长和短半轴的长
(Ⅱ)求椭圆的焦点和顶点坐标.
分析 (Ⅰ)将椭圆方程转成标准方程,求得a和b的值;
(Ⅱ)由(Ⅰ),利用椭圆简单几何性质,即可求得椭圆的焦点和顶点坐标.
解答 解:(Ⅰ)由16x2+25y2=400,转化成标准方程:$\frac{x^2}{25}+\frac{y^2}{16}=1$,…(2分)
则长轴长2a=10,短半轴长b=4…(6分)
(Ⅱ)焦点坐标(-3,0),(3,0),顶点坐标(-5,0),(5,0);(0,4)(0,-4),
点评 本题考查椭圆的标准方程及简单几何性质,考查转化思想,属于基础题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
2.如果z是3+4i的共轭复数,则z对应的向量$\overrightarrow{OA}$的模是( )
| A. | 1 | B. | $\sqrt{7}$ | C. | $\sqrt{13}$ | D. | 5 |
3.下列给出的函数中,既不是奇函数也不是偶函数的是( )
| A. | $y=\frac{2}{x}$ | B. | y=x3 | C. | y=-x2 | D. | $y=\sqrt{x}$ |
4.“$\left\{{x\left|{\frac{1}{x}≤1}\right.}\right\}$”是“{x|lnx≥0}”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
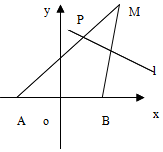 已知A点坐标为$(-2\sqrt{3},0)$,B点坐标为$(2\sqrt{3},0)$,且动点M到A点的距离是8,线段MB的垂直平分线l交线段MA于点P.
已知A点坐标为$(-2\sqrt{3},0)$,B点坐标为$(2\sqrt{3},0)$,且动点M到A点的距离是8,线段MB的垂直平分线l交线段MA于点P.