题目内容
9.直线y=kx+1(k∈R)与椭圆$\frac{x^2}{5}+\frac{y^2}{m}=1$恒有两个公共点,则m的取值范围为( )| A. | (1,+∞) | B. | [1,+∞) | C. | (1,5)∪(5,+∞) | D. | [1,5)∪(5,+∞) |
分析 直线方程与椭圆方程联立化为:(m+5k2)x2+10kx+5-5m=0.根据直线与椭圆恒有两个公共点,可得△>0,m>0,m≠5.解出即可得出.
解答 解:联立$\left\{\begin{array}{l}{y=kx+1}\\{\frac{{x}^{2}}{5}+\frac{{y}^{2}}{m}=1}\end{array}\right.$,化为:(m+5k2)x2+10kx+5-5m=0.
∵直线与椭圆恒有两个公共点,∴△=100k2-4(m+5k2)(5-5m)>0,m>0,m≠5.
化为:m2-(1-5k2)m>0,m>0,m≠5.
∴m>1-5k2,m>0,m≠5,又k∈R,
∴m>1,且m≠5.
∴m的取值范围为(1,5)∪(5,+∞).
故选:C.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交与判别式的关系、不等式的解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.函数f(x)=ln(x2-1)的定义域为( )
| A. | (-∞,-1)∪(1,+∞) | B. | (-∞,1)∪(1,+∞) | C. | (1,+∞) | D. | (0,1) |
18.若集合A={-2,0,1,3},B={-1,1,3}则A∪B元素的个数为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
 如图,正八面体P-ABCD-Q由两个棱长都为a的正四棱锥拼接而成.
如图,正八面体P-ABCD-Q由两个棱长都为a的正四棱锥拼接而成.

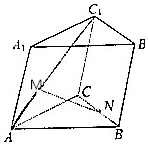 如图所示,已知斜三棱柱ABC-A1B1C1,点M,N分别在AC1和BC上,且满足$\overrightarrow{AM}$=k$\overrightarrow{A{C}_{1}}$,$\overrightarrow{BN}$=k$\overrightarrow{BC}$(0≤k≤1).
如图所示,已知斜三棱柱ABC-A1B1C1,点M,N分别在AC1和BC上,且满足$\overrightarrow{AM}$=k$\overrightarrow{A{C}_{1}}$,$\overrightarrow{BN}$=k$\overrightarrow{BC}$(0≤k≤1).