题目内容
2.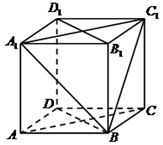 在正方体ABCD-A1B1C1D1中:
在正方体ABCD-A1B1C1D1中:(Ⅰ)求证:AC∥平面A1BC1;
(Ⅱ)求证:平面A1BC1⊥平面BB1D1D.
分析 (Ⅰ)证明四边形ACC1A1为平行四边形,可得AC∥A1C1,即可证明AC∥平面A1BC1;
(Ⅱ)证明A1C1⊥平面BB1D1D,即可证明平面A1BC1⊥平面BB1D1D.
解答 证明:(Ⅰ)因为AA1∥CC1,所以四边形ACC1A1为平行四边形,…(2分)
所以AC∥A1C1,又A1C1?平面A1BC1,AC?平面A1BC1,AC∥平面A1BC1; …(5分)
(Ⅱ)易知A1C1⊥B1D1,因为BB1⊥平面A1B1C1D1,所以BB1⊥A1C1,…(7分)
因为BB1∩B1D1=B1,所以A1C1⊥平面BB1D1D,
因为A1C1?平面A1BC1,所以平面A1BC1⊥平面BB1D1D.…(10分)
点评 本题考查线面平行的判定、考查线面垂直、面面垂直的判定,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.已知全集U={0,1,2,3,4},集合A={1,2},B={0,2,4},则(∁UA)∩B等于( )
| A. | {0,4} | B. | {0,3,4} | C. | {0,2,3,4} | D. | {2} |
17.已知b>0,log3b=a,log6b=c,3d=6,则下列等式成立的是( )
| A. | a=2c | B. | d=ac | C. | a=cd | D. | c=ad |
12.已知在△ABC中,∠ACB=$\frac{π}{2}$,AB=2BC,现将△ABC绕BC所在直线旋转到△PBC,设二面角P-BC-A大小为θ,PB与平面ABC所成角为α,PC与平面PAB所成角为β,若0<θ<π,则( )
| A. | $α≤\frac{π}{3}$且$sinβ≤\frac{{\sqrt{3}}}{3}$ | B. | $α≤\frac{π}{3}$且$sinβ<\frac{{\sqrt{3}}}{3}$ | C. | $α≤\frac{π}{6}$且$β≥\frac{π}{3}$ | D. | $α≤\frac{π}{6}$且$β<\frac{π}{3}$ |
 已知如图正四面体SABC的侧面积为$48\sqrt{3}$,O为底面正三角形ABC的中心.
已知如图正四面体SABC的侧面积为$48\sqrt{3}$,O为底面正三角形ABC的中心.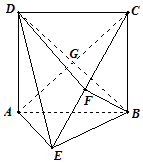 如图,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,BD∩AC=G.
如图,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,BD∩AC=G.