题目内容
设a,b为正实数,则“a<b”是“a-
<b-
”成立的( )
| 1 |
| a |
| 1 |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、既不充分也不必要条件 |
| D、充要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:由0<a<b容易得到a-
<b-
,而a-
<b-
时,根据a>0,b>0容易得到ab(a-b)<b-a,所以a<b,所以最后得出a<b是a-
<b-
的充要条件.
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
解答:
解:(1)∵0<a<b;
∴
>
,-
<-
;
∴a-
<b-
;
(2)若a-
<b-
;
∵a,b>0;
a2b-b<ab2-a;
∴ab(a-b)<b-a;
∴b-a>0;
∴a<b;
∴综上得a<b是a-
<b-
的充要条件.
故选:D.
∴
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
∴a-
| 1 |
| a |
| 1 |
| b |
(2)若a-
| 1 |
| a |
| 1 |
| b |
∵a,b>0;
a2b-b<ab2-a;
∴ab(a-b)<b-a;
∴b-a>0;
∴a<b;
∴综上得a<b是a-
| 1 |
| a |
| 1 |
| b |
故选:D.
点评:考查0<a<b时,
,
的大小关系,以及充分条件,必要条件,充要条件的概念.
| 1 |
| a |
| 1 |
| b |

练习册系列答案
相关题目
已知集合A={x|x>0},B={x|x≥1},则A∩(∁RB)等于( )
| A、{x|x>1} |
| B、{x|x>0} |
| C、{x|0<x<1} |
| D、{x|x<1} |
若实数x,y满足
,则
的最小值是( )
|
| y-3 |
| x-2 |
| A、2 | ||
B、
| ||
| C、1 | ||
D、
|
设数列
,
,2
,
,…,则2
是这个数列的( )
| 2 |
| 5 |
| 2 |
| 11 |
| 5 |
| A、第6项 | B、第7项 |
| C、第8项 | D、第9项 |
若θ是任意实数,则方程x2+4y2sinθ=1所表示的曲线一定不是( )
| A、抛物线 | B、双曲线 | C、直线 | D、圆 |
如图是某样本数据的茎叶图,则该样本数据的众数为( )
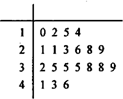

| A、10 | B、21 | C、35 | D、46 |
已知集合M={x||x-1|<1},集合N={x|x2-2x<3},则M∩∁RN=( )
| A、{x|0<x<2} |
| B、{x|-1<x<2} |
| C、{x|-1<x≤0或2≤x<3} |
| D、∅ |