题目内容
6．函数y=sinx-$\frac{1}{2}$cosx（x∈[0，$\frac{π}{2}$]）的最大值为1．分析 利用导数研究函数的单调性，再利用函数的单调性求得函数y的最大值．
解答 解：∵函数y=sinx-$\frac{1}{2}$cosx（x∈[0，$\frac{π}{2}$]），故函数的导数y′=cosx+$\frac{1}{2}$sinx＞0，
故函数y在[0，$\frac{π}{2}$]上单调递增，故当x=$\frac{π}{2}$时，函数y取得最大值为1，
故答案为：1．
点评 本题主要考查利用导数研究函数的单调性，求三角函数的最值，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
14．在△ABC中，角A，B，C所对边分别为a，b，c，且（2b-a）•cosC=ccosA，c=3，sinA+sinB=2$\sqrt{6}$sinAsinB，则△ABC的面积为（ ）
| A． | $\frac{3\sqrt{3}}{8}$ | B． | 2 | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{3\sqrt{3}}{4}$ |
1．在△ABC中，已知cosA=$\frac{3}{5}$，cosB=$\frac{12}{13}$，则cosC的值为（ ）
| A． | $\frac{56}{65}$ | B． | -$\frac{56}{65}$ | C． | -$\frac{16}{65}$ | D． | $\frac{56}{65}$或-$\frac{16}{65}$ |
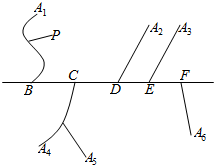如图，一条公路的两侧有六个村庄，要建一个车站，要求到六个村庄的路程之和最小，应该选在哪里最合适？如果在P的地方增加一个村庄，并且沿地图的虚线修了一条小路，那么这时车站设在什么地方好？