题目内容
已知函数f（x）为二次函数，且满足f（1）=1，f（x）有两个零点为0和2，设F（x）=
（1）求函数f（x）和F（x）的解析式；
（2）在答卷给定的坐标系中画出函数F（x）的图象；（不需列表）
（3）根据图象讨论关于x的方程F（x）-k=0（k∈R）根的个数（只需写出结果，不要解答过程）
|
（1）求函数f（x）和F（x）的解析式；
（2）在答卷给定的坐标系中画出函数F（x）的图象；（不需列表）
（3）根据图象讨论关于x的方程F（x）-k=0（k∈R）根的个数（只需写出结果，不要解答过程）
考点：根的存在性及根的个数判断,函数解析式的求解及常用方法
专题：计算题,作图题,函数的性质及应用
分析：（1）由题意，设f（x）=ax（x-2）；从而写出f（x）=-x（x-2）；F（x）=
；
（2）作函数图象，
（3）由图象可知确定方程的根的个数．
|
（2）作函数图象，
（3）由图象可知确定方程的根的个数．
解答：
解：（1）由题意，设f（x）=ax（x-2）；
则由f（1）=1得，-a=1；
解得a=-1；
故f（x）=-x（x-2）；
F（x）=
；
（2）作图如下，
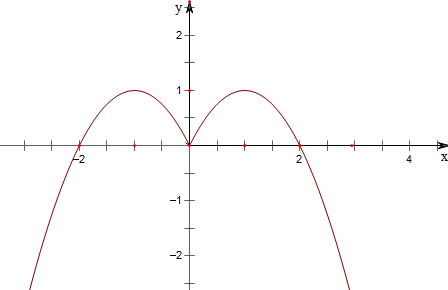
（3）由图象可知，
当k＞1时，关于x的方程F（x）-k=0（k∈R）有0个根，
当k=1时，关于x的方程F（x）-k=0（k∈R）有2个根，
当0＜k＜1时，关于x的方程F（x）-k=0（k∈R）4个根，
当k=0时，关于x的方程F（x）-k=0（k∈R）有3个根，
当k＜0时，关于x的方程F（x）-k=0（k∈R）有2个根．
则由f（1）=1得，-a=1；
解得a=-1；
故f（x）=-x（x-2）；
F（x）=
|
（2）作图如下，
（3）由图象可知，
当k＞1时，关于x的方程F（x）-k=0（k∈R）有0个根，
当k=1时，关于x的方程F（x）-k=0（k∈R）有2个根，
当0＜k＜1时，关于x的方程F（x）-k=0（k∈R）4个根，
当k=0时，关于x的方程F（x）-k=0（k∈R）有3个根，
当k＜0时，关于x的方程F（x）-k=0（k∈R）有2个根．
点评：本题考查了函数解析式的求法及作图能力的培养，属于基础题．
练习册系列答案
新课标阶梯阅读训练系列答案
口算心算速算应用题系列答案
相关题目
已知向量
=(-3，4)，则下列能使
=λ
+μ
(λ、μ∈R)成立的一组向量
，
是（ ）
| a |
| a |
| e1 |
| e2 |
| e1 |
| e2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
如程序框图所示，已知集合A={x|框图中输出的x值}，B={y|框图中输出的y值}；当x=1时，A∩B=（ ）| A、∅ | B、{3} |
| C、{3，5} | D、{1，3，5} |