题目内容
 函数y=f(x)(x∈R)的图象如右图所示,下列说法正确的有
函数y=f(x)(x∈R)的图象如右图所示,下列说法正确的有①函数y=f(x)满足f(-x)=-f(x);
②函数y=f(x)满足f(x+2)=f(-x);
③函数y=f(x)满足f(-x)=f(x);
④函数y=f(x)满足f(x+2)=f(x).
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:根据函数y=f(x)的图象得出函数是奇函数,判断①正确、④错误;
函数y=f(x)是周期为4的函数,判断②正确、③错误.
函数y=f(x)是周期为4的函数,判断②正确、③错误.
解答:
解:根据函数y=f(x)(x∈R)的图象,知;
函数y=f(x)的图象关于原点对称,是奇函数,且满足f(-x)=-f(x),∴①正确;
函数y=f(x)的周期为4,满足f(x+2)=f(-x)=-f(x),∴②正确;
函数y=f(x)的图象不关于y轴对称,即f(x)不是偶函数,且f(-x)≠f(x),∴③错误.
函数y=f(x)的周期为4,满足f(x+4)=-f(x+2)=f(x),∴④错误;
综上,正确的说法是①②.
故答案为:①②.
函数y=f(x)的图象关于原点对称,是奇函数,且满足f(-x)=-f(x),∴①正确;
函数y=f(x)的周期为4,满足f(x+2)=f(-x)=-f(x),∴②正确;
函数y=f(x)的图象不关于y轴对称,即f(x)不是偶函数,且f(-x)≠f(x),∴③错误.
函数y=f(x)的周期为4,满足f(x+4)=-f(x+2)=f(x),∴④错误;
综上,正确的说法是①②.
故答案为:①②.
点评:本题考查了根据函数图象判断函数的周期性与奇偶性的应用问题,是基础题目.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
若M={x|-2≤x<2},N={x|y=log2(x-1)},则M∩N=( )
| A、{x|-2≤x<0} |
| B、{x|-1<x<0} |
| C、{-2,0} |
| D、{x|1<x<2} |
双曲线x2-y2=2的离心率是( )
| A、1 | ||
B、
| ||
| C、2 | ||
D、2
|
 从某小学随机抽取100分学生,将们们的身高(单位:厘米)数据绘制成频率分布直方图(如图),若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取20人参加一项活动,则身高在[120,130)内的学生中选取的人数应为( )
从某小学随机抽取100分学生,将们们的身高(单位:厘米)数据绘制成频率分布直方图(如图),若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取20人参加一项活动,则身高在[120,130)内的学生中选取的人数应为( )| A、8 | B、12 | C、10 | D、30 |
设0<a<1,关于x的不等式a (t2-1)x2-(t-1)x-1>1的解集为R,则实数t的取值范围是( )
A、(-
| ||
| B、(-1,1) | ||
C、(-
| ||
| D、[-1,1] |
若函数y=ax+m-1(a>0)的图象经过第一、三和四象限,则( )
| A、a>1 |
| B、0<a<1且m>0 |
| C、a>1 且m<0 |
| D、0<a<1 |
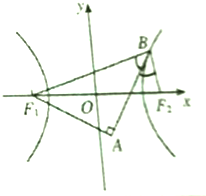 如图,F1、F2分别是双曲线x2-y2=1的左右焦点,点A的坐标是(
如图,F1、F2分别是双曲线x2-y2=1的左右焦点,点A的坐标是(