题目内容
 从某小学随机抽取100分学生,将们们的身高(单位:厘米)数据绘制成频率分布直方图(如图),若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取20人参加一项活动,则身高在[120,130)内的学生中选取的人数应为( )
从某小学随机抽取100分学生,将们们的身高(单位:厘米)数据绘制成频率分布直方图(如图),若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取20人参加一项活动,则身高在[120,130)内的学生中选取的人数应为( )| A、8 | B、12 | C、10 | D、30 |
考点:频率分布直方图
专题:概率与统计
分析:先求出身高在[120,130)、[130,140)和[140,150]的频数,
再计算用分层抽样方法选取身高在[120,130)内的学生数.
再计算用分层抽样方法选取身高在[120,130)内的学生数.
解答:
解:根据频率分布直方图,得;
身高在[120,130)的频率为0.030×10=0.3,频数是0.3×100=30;
身高在[130,140)的频率为0.020×10=0.2,频数是0.2×100=20;
身高在[140,150]的频率为0.010×10=0.1,频数是0.1×100=10;
在这三组学生中,用分层抽样的方法选取20人参加一项活动,
身高在[120,130)内的学生中选取的人数为20×
=10.
故选:C.
身高在[120,130)的频率为0.030×10=0.3,频数是0.3×100=30;
身高在[130,140)的频率为0.020×10=0.2,频数是0.2×100=20;
身高在[140,150]的频率为0.010×10=0.1,频数是0.1×100=10;
在这三组学生中,用分层抽样的方法选取20人参加一项活动,
身高在[120,130)内的学生中选取的人数为20×
| 30 |
| 30+20+10 |
故选:C.
点评:本题考查了频率分布直方图的应用问题,也考查了分层抽样方法的应用问题,是基础题目.

练习册系列答案
相关题目
已知集合A={x|x2-2x-3=0},B={x|x2+x-12<0},则A∩B等于( )
| A、{-1} | B、{-3} |
| C、{1} |
函数y=
的定义域为( )
3x-
|
| A、[0,+∞) | ||
B、[
| ||
| C、[-1,+∞) | ||
| D、(-∞,-1] |
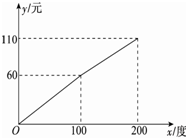 某供电公司为了合理分配电力,采用分段计算电费政策,月用电量x(度)与相应电费y(元)之间的函数关系的图象如图所示.
某供电公司为了合理分配电力,采用分段计算电费政策,月用电量x(度)与相应电费y(元)之间的函数关系的图象如图所示. 函数y=f(x)(x∈R)的图象如右图所示,下列说法正确的有
函数y=f(x)(x∈R)的图象如右图所示,下列说法正确的有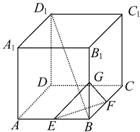 在棱长为1的正方体AC1中,E为AB的中点,点P为侧面BB1C1C内一动点(含边界),若动点P始终满足PE⊥BD1,则动点P的轨迹的长度为( )
在棱长为1的正方体AC1中,E为AB的中点,点P为侧面BB1C1C内一动点(含边界),若动点P始终满足PE⊥BD1,则动点P的轨迹的长度为( )