题目内容
两所学校分别有2名,3名学生获奖,这5名学生要排成一排合影,则存在同校学生排在一起的概率为 .
考点:古典概型及其概率计算公式
专题:概率与统计
分析:利用对立事件概率计算公式能求出结果.
解答:
解:由已知得存在同校学生排在一起的概率为:
P=1-
=
.
故答案为:
.
P=1-
| 3!×2! |
| 5! |
| 9 |
| 10 |
故答案为:
| 9 |
| 10 |
点评:本题考查概率的求法,是基础题,解题时要认真审题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数y=
的定义域为( )
3x-
|
| A、[0,+∞) | ||
B、[
| ||
| C、[-1,+∞) | ||
| D、(-∞,-1] |
若已知两个变量x 和y 之间具有线性相关系,4 次试验的观测数据如下:
经计算得回归方程
=bx+a系数b=0.7,则a等于( )
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
| ∧ |
| y |
| A、0.34 | B、0.35 |
| C、0.45 | D、0.44 |

 函数y=f(x)(x∈R)的图象如右图所示,下列说法正确的有
函数y=f(x)(x∈R)的图象如右图所示,下列说法正确的有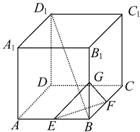 在棱长为1的正方体AC1中,E为AB的中点,点P为侧面BB1C1C内一动点(含边界),若动点P始终满足PE⊥BD1,则动点P的轨迹的长度为( )
在棱长为1的正方体AC1中,E为AB的中点,点P为侧面BB1C1C内一动点(含边界),若动点P始终满足PE⊥BD1,则动点P的轨迹的长度为( ) 如图,l1l2是通过某市开发区中心O的南北和东西走向的两条道路,连接M,N两地的铁路是一段抛物线弧,它所在的抛物线关于直线l1对称,M到l1,l2的距离分别是2km,4km;N到l1,l2的距离分别是3km,9km.该市拟在点O的正北方向建设一座工厂,要求厂址到点O的距离大于5km,而不超过8km,并且铁路上任意一点到工厂的距离不能小于
如图,l1l2是通过某市开发区中心O的南北和东西走向的两条道路,连接M,N两地的铁路是一段抛物线弧,它所在的抛物线关于直线l1对称,M到l1,l2的距离分别是2km,4km;N到l1,l2的距离分别是3km,9km.该市拟在点O的正北方向建设一座工厂,要求厂址到点O的距离大于5km,而不超过8km,并且铁路上任意一点到工厂的距离不能小于