题目内容

函数y=4sin（2x-
π
6
）的图象的一个对称中心是（　　）
A、（
π
12
，0）
B、（
π
3
，0）
C、（-
π
6
，0）
D、（
π
6
，0）
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：令2x-
π
6
=kπ，k∈z，可得对称中心的横坐标 x=
kπ
2
+
π
12
，k∈z，又纵坐标等于0，可得对称中心的坐标，从而求得结果．
解答： 解：函数y=4sin（2x-
π
6
）是图象的对称中心是图象和x轴的交点，
令2x-
π
6
=kπ，k∈z，可得对称中心的横坐标x=
kπ
2
+
π
12
，k∈z，
故k=0时，函数y=4sin（2x-
π
6
）是图象的一个对称中心是（
π
12
，0），
 故选：A．
点评：本题考查正弦函数的对称性，求得对称中心的横坐标为x=
kπ
2
+
π
12
，k∈z是解题的关键．
练习册系列答案
相关题目
每次用相同体积的清水洗一件衣物，且每次能洗去污垢的
3
4
，若洗n次后，存在的污垢在1%以下，则n的最小值为
 
．
下列叙述中，正确的个数是（　　）
①命题p：“?x∈R，x2-2≥0”的否定形式为￢p：“?x∈R，x2-2＜0”；
②O是△ABC所在平面上一点，若
OA
•
OB
=
OB
•
OC
=
OC
•
OA
，则O是△ABC的垂心；
③“M＞N”是“（
2
3
）M＞（
2
3
）N”的充分不必要条件；
④命题“若x2-3x-4=0，则x=4”的逆否命题为“若x≠4，则x2-3x-4=0”．
A、1B、2C、3D、4
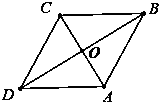
如图，在菱形ABCD中，∠DAB=120°，则以下说法错误的是（　　）
A、与
AB
相等的向量只有一个（不含
AB
）
B、与
AB
的模相等的向量有9个（不含
AB
）
C、
BD
的模恰为
DA
模的
3
倍
D、
CB
与
DA
不共线
若函数y=ax+2-2（a＞0且a≠1）的图象恒过定点A，若点A在直线
x
m
+
y
n
=-1上，且m＞0，n＞0，则m+2n的最小值为（　　）
A、7B、8C、9D、10
已知△ABC的顶点A（0，0），B（4，0），且AC边上的中线BD的长为3，则顶点C的轨迹方程是（　　）
A、（x-8）2+y2=36（y≠0）
B、（x-4）2+y2=9（y≠0）
C、x2+y2=9（y≠0）
D、3x+4y-12=0（y≠0）
圆（x+2）2+（y+1）2=4关于x轴对称的圆的方程为（　　）
A、（x-2）2+（y+1）2=4
B、（x+2）2+（y-1）2=4
C、（x-2）2+（y-1）2=4
D、（x+2）2+（y+1）2=4
1426和1643的最大公约数是（　　）
A、34B、12C、93D、31
已知α是第四象限的角，且sinα•cosα=-
12
25
，则sinα-cosα=（　　）
A、-
49
25
B、
49
25
C、
7
5
D、-
7
5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网