题目内容
设复数z=
+(1-i)2且满足z2+3z+1=a+bi(a,b∈R).求(a+b)2015的值.
| 1+i |
| 1-i |
考点:复数代数形式的混合运算
专题:数系的扩充和复数
分析:由复数的代数形式的乘除运算得到z=-i,由此利用z2+3z+1=a+bi,求出a=0,b=-3,从而能求出结果.
解答:
解:z=
+(1-i)2
=
+1-2i+i2
=
-2i
=i-2i=-i,
∵z2+3z+1=a+bi,
∴(-i)2+3(-i)+1=a+bi,
∴-3i=a+bi,∴a=0,b=-3,
∴(a+b)2015=(-3)2015=-32015.
| 1+i |
| 1-i |
=
| (1+i)2 |
| (1-i)(1+i) |
=
| 1+2i+i2 |
| 2 |
=i-2i=-i,
∵z2+3z+1=a+bi,
∴(-i)2+3(-i)+1=a+bi,
∴-3i=a+bi,∴a=0,b=-3,
∴(a+b)2015=(-3)2015=-32015.
点评:本题考查代数式的值的求法,解题时要认真审题,注意复数的代数形式的乘除运算的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
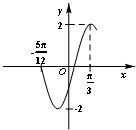 函数f(x)=2sin(ωx+φ)(ω>0,-
函数f(x)=2sin(ωx+φ)(ω>0,-| π |
| 2 |
| π |
| 2 |
A、2,-
| ||
B、4,
| ||
C、4,-
| ||
D、2,-
|
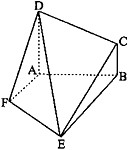 如图,四边形ABCD和ABEF都是直角梯形,AD∥BC,AF∥BE,∠DAB=∠FAB=90°,且平面ABCD⊥平面ABEF,DA=AB=BE=2,BC=1.
如图,四边形ABCD和ABEF都是直角梯形,AD∥BC,AF∥BE,∠DAB=∠FAB=90°,且平面ABCD⊥平面ABEF,DA=AB=BE=2,BC=1.