题目内容
等差数列{an}的前项n和为Sn,满足S35=S3992,
=(1,an),
=(2014,a2014),则
•
的值为( )
| a |
| b |
| a |
| b |
| A、2014 | B、-2014 |
| C、1 | D、0 |
考点:平面向量数量积的运算
专题:等差数列与等比数列,平面向量及应用
分析:由性质:若Sm=Sn,则Sm+n=0,得S4027=0,从而得到a2014=0,在代入计算即可.
解答:
解:由性质:若Sm=Sn,则Sm+n=0,知
∵S35=S3992,得S4027=0,
∴a1+a4027=2a2014=0,
即a2014=0.
∴
•
=2014+ana2014=2014.
故选:A.
∵S35=S3992,得S4027=0,
∴a1+a4027=2a2014=0,
即a2014=0.
∴
| a |
| b |
故选:A.
点评:本题解题的关键是对等差数列中的性质:若Sm=Sn,则Sm+n=0的掌握,否则所带来的计算很繁琐.

练习册系列答案
相关题目
设x∈R,则“x2>4”是“x>2”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
若抛物线x2=2py(p>0)的焦点与双曲线
-x2=1的一个焦点重合,则p的值为( )
| y2 |
| 3 |
| A、-2 | B、2 | C、-4 | D、4 |
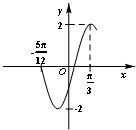 函数f(x)=2sin(ωx+φ)(ω>0,-
函数f(x)=2sin(ωx+φ)(ω>0,-| π |
| 2 |
| π |
| 2 |
A、2,-
| ||
B、4,
| ||
C、4,-
| ||
D、2,-
|
△ABC中,a=x,b=2,∠B=60°,则当△ABC有两个解时,x的取值范围是( )
A、x>
| ||||
B、x<2或x>
| ||||
| C、x<2 | ||||
D、2<x<
|
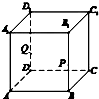 已知如图所示的正方体ABCD-A1B1C1D1,点P、Q分别在棱BB1、DD1上,且
已知如图所示的正方体ABCD-A1B1C1D1,点P、Q分别在棱BB1、DD1上,且