题目内容
19.已知F1,F2分别是椭圆mx2+y2=m(0<m<1)的左、右焦点,P为椭圆上任意一点,若$\frac{|\overrightarrow{P{F}_{2}}{|}^{2}+|\overrightarrow{P{F}_{1}}|}{|\overrightarrow{P{F}_{1}}|}$的最小值为$\frac{4}{3}$,则椭圆的离心率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
分析 由题意画出图形,再由$\frac{|\overrightarrow{P{F}_{2}}{|}^{2}+|\overrightarrow{P{F}_{1}}|}{|\overrightarrow{P{F}_{1}}|}$的最小值为$\frac{4}{3}$,结合对勾函数的单调性可知当$|\overrightarrow{P{F}_{1}}|$取最大值为a+c时成立,求得c值,则椭圆离心率可求.
解答 解:令|$\overrightarrow{P{F}_{1}}$|=s,|$\overrightarrow{P{F}_{2}}$|=t,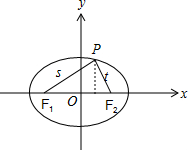
则$\frac{|\overrightarrow{P{F}_{2}}{|}^{2}+|\overrightarrow{P{F}_{1}}|}{|\overrightarrow{P{F}_{1}}|}$为$\frac{{t}^{2}+s}{s}$,其最小值为$\frac{4}{3}$,
则$\frac{{t}^{2}}{s}$的最小值为$\frac{1}{3}$.
由椭圆mx2+y2=m,得${x}^{2}+\frac{{y}^{2}}{m}=1$,
∵0<m<1,∴椭圆的长轴长为2.
∴$\frac{(2-s)^{2}}{s}=\frac{4}{s}+s-4≥\frac{1}{3}$,
∴$\frac{4}{s}+s≥\frac{13}{3}$,
由$\frac{4}{s}+s=\frac{13}{3}$,解得s=$\frac{4}{3}$或s=3(舍).
由对勾函数的单调性可知,当s有最大值为a+c=$\frac{4}{3}$时,$\frac{{t}^{2}+s}{s}$有最小值为$\frac{4}{3}$,
即1+c=$\frac{4}{3}$,得c=$\frac{1}{3}$.
∴椭圆的离心率e=$\frac{c}{a}=\frac{1}{3}$.
故选:B.
点评 本题考查椭圆的简单性质,考查了椭圆定义的应用,训练了利用“对勾函数”的单调性求函数最值,是中档题.

| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
| A. | f($\frac{π}{6}$)>$\sqrt{2}$f($\frac{π}{4}$) | B. | $\sqrt{2}$sin1•f(1)>f($\frac{π}{4}$) | C. | f($\frac{π}{6}$)>$\sqrt{3}$f($\frac{π}{3}$) | D. | $\sqrt{2}$f($\frac{π}{4}$)>$\sqrt{3}$f($\frac{π}{3}$) |
| A. | 40 | B. | 60 | C. | 80 | D. | 100 |
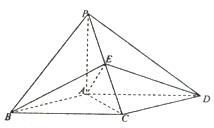 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,AP=AB=AC=a,AD=$\sqrt{2}$a,PA⊥底面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,AP=AB=AC=a,AD=$\sqrt{2}$a,PA⊥底面ABCD.