题目内容
方程f(x)=x的根称为f(x)的不动点,若函数f(x)=
有唯一不动点,且x1=2,xn+1=
(n∈N+),则log
(x2014-1)=( )
| x |
| a(x+2) |
| 1 | ||
f(
|
| 1 |
| 2 |
| A、2014 | B、2013 |
| C、1 | D、0 |
考点:对数的运算性质
专题:函数的性质及应用
分析:函数f(x)=
有唯一不动点?
=x有唯一实数根,化为ax2+(2a-1)x=0,由于a≠0,可得△=0,解得a=
.f(x)=
.由于x1=2,xn+1=
,可得xn+1-1=
(xn-1),再利用等比数列的通项公式与对数的运算性质即可得出.
| x |
| a(x+2) |
| x |
| a(x+2) |
| 1 |
| 2 |
| 2x |
| x+2 |
| 1 | ||
f(
|
| 1 |
| 2 |
解答:
解:函数f(x)=
有唯一不动点,∴
=x有唯一实数根,
化为ax2+(2a-1)x=0,∵a≠0,∴△=(2a-1)2-0=0,解得a=
.
∴f(x)=
.
∵且x1=2,xn+1=
,
∴xn+1=
=
xn+
,
∴xn+1-1=
(xn-1),
∴数列{xn-1}是等比数列,
∴xn-1=(2-1)×(
)n-1,
∴xn-1=(
)n-1.
∴log
(x2014-1)=log
(
)2013=2013.
故选:B.
| x |
| a(x+2) |
| x |
| a(x+2) |
化为ax2+(2a-1)x=0,∵a≠0,∴△=(2a-1)2-0=0,解得a=
| 1 |
| 2 |
∴f(x)=
| 2x |
| x+2 |
∵且x1=2,xn+1=
| 1 | ||
f(
|
∴xn+1=
| ||
2×
|
| 1 |
| 2 |
| 1 |
| 2 |
∴xn+1-1=
| 1 |
| 2 |
∴数列{xn-1}是等比数列,
∴xn-1=(2-1)×(
| 1 |
| 2 |
∴xn-1=(
| 1 |
| 2 |
∴log
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故选:B.
点评:本题考查了新定义“不动点”、等比数列的通项公式与对数的运算性质,考查了等价转化能力,考查了推理能力与计算能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)是R上的可导函数,f(x)的导数f′(x)的图象如图,则下列结论正确的是( )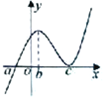

| A、a,c分别是极大值点和极小值点 |
| B、b,c分别是极大值点和极小值点 |
| C、f(x)在区间(a,c)上是增函数 |
| D、f(x)在区间(b,c)上是减函数 |