题目内容
在xOy平面上有一系列的点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…,对于所有正整数n,点Pn位于函数y=x2(x≥0)的图象上,以点Pn为圆心的圆Pn与x轴相切,且圆Pn与圆Pn+1又彼此外切,且xn+1<xn.则
nxn等于 .
| lim |
| n→∞ |
考点:数列的极限
专题:计算题,直线与圆
分析:由题意圆Pn与Pn+1彼此外切,利用两圆外切等价于两圆心距等于圆的半径和,化简出数列{xn}的递推关系,进而得到数列{xn}的通项公式xn及nxn,由数列极限的运算性质可求答案.
解答:
解:圆Pn与Pn+1彼此外切,令rn为圆Pn的半径,
∴|PnPn+1|=rn+rn+1即
=yn+yn+1,
两边平方并化简得(xn-xn+1)2=4ynyn+1,
由题意得,圆Pn的半径rn=yn=xn2,(xn-xn+1)2=4xn2xn+12
∵xn>xn+1>0,∴xn-xn+1=2xnxn+1,
即
-
=2(n∈N*),
∴数列{
}是以
为首项,以2为公差的等差数列,∴
=
+(n-1)×2=2n-2+
,
∴xn=
,nxn=
,
nxn=
=
,
故答案为:
.
∴|PnPn+1|=rn+rn+1即
| (xn-xn+1)2+(yn-yn+1)2 |
两边平方并化简得(xn-xn+1)2=4ynyn+1,
由题意得,圆Pn的半径rn=yn=xn2,(xn-xn+1)2=4xn2xn+12
∵xn>xn+1>0,∴xn-xn+1=2xnxn+1,
即
| 1 |
| xn+1 |
| 1 |
| xn |
∴数列{
| 1 |
| xn |
| 1 |
| x1 |
| 1 |
| xn |
| 1 |
| x1 |
| 1 |
| x1 |
∴xn=
| 1 | ||
2n-2+
|
| n | ||
2n-2+
|
| lim |
| n→∞ |
| lim |
| n→∞ |
| n | ||
2n-2+
|
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:此题重点考查了两元相外切的等价条件,还考查了有关数列的递推关系求其通项公式,考查了数列极限的运算性质.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
设函数f(x)=
,则f(log23)=( )
|
A、
| ||
B、
| ||
C、
| ||
D、-
|
 从一个棱长为3的正方体中切去一些部分,得到一个几何体,其三视图如图,则该几何体的体积为( )
从一个棱长为3的正方体中切去一些部分,得到一个几何体,其三视图如图,则该几何体的体积为( )| A、3 | B、7 | C、9 | D、18 |
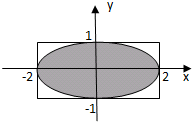 已知椭圆的面积公式为S=πab(其中a为椭圆的长半轴长,b为椭圆的短半轴长),在如图所示矩形框内随机选取400个点,估计这400个点中属于阴影部分的点约有( )
已知椭圆的面积公式为S=πab(其中a为椭圆的长半轴长,b为椭圆的短半轴长),在如图所示矩形框内随机选取400个点,估计这400个点中属于阴影部分的点约有( )| A、100个 | B、200个 |
| C、300个 | D、400个 |
已知数列{an}的首项a1=1,且an=2an-1+1(n≥2),则a6=( )
| A、15 | B、31 | C、62 | D、63 |
对于函数f(x)=x2+|x-a|+1(a∈R),下列结论中正确的是( )
| A、当a≥0时,f(x)在(-∞,0)上单调递减 | ||
| B、当a≤0时,f(x)在(-∞,0)上单调递减 | ||
C、当a≥
| ||
D、当a≤
|