题目内容
12.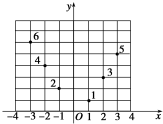 如图所示,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列{an}(n∈N*)的前12项,如表所示.
如图所示,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列{an}(n∈N*)的前12项,如表所示.| a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | a11 | a12 |
| x1 | y1 | x2 | y2 | x3 | y3 | x4 | y4 | x5 | y5 | x6 | y6 |
| A. | 1 003 | B. | 1 005 | C. | 1 006 | D. | 2 010 |
分析 奇数项为1,-1,2,-2…,发现a2n-1+a2n+1=0,偶数项为1,2,3…,所以a2n=n.当2n-1=2009时,n=1005,故a2009+a2011=0.当2n=2010,a2010=1005.
解答 解:奇数项,偶数项分开看,
奇数项为1,-1,2,-2…,发现a2n-1+a2n+1=0,
偶数项为1,2,3…,所以a2n=n
当2n-1=2009时,n=1005,故a2009+a2011=0.
当2n=2010,a2010=1005.
∴a2009+a2010+a2011=1005.
故选B.
点评 本题考查数列的性质和应用,解题的关键是明确题意,找出数字的变化规律.

练习册系列答案
相关题目
14.设变量x、y满足约束条件$\left\{\begin{array}{l}3x+y-6≥0\\ x-y-2≤0\\ y-3≤0\end{array}\right.$,则目标函数z=4x+y的最小值为( )
| A. | -6 | B. | 6 | C. | 7 | D. | 8 |
7.抛物线y2=8x的焦点坐标是( )
| A. | (-2,0) | B. | (0,-2) | C. | (2,0) | D. | (0,2) |
17.已知,焦点在x轴上的椭圆的上、下顶点分别为B2、B1,左焦点和右顶点分别为F、A1.经过点B2的直线l与以椭圆的中心为顶点、B2为焦点的抛物线交于A、B两点,且点B2恰为线段AB的三等分点,直线l1过点B1且垂直于y轴,线段AB的中点M到直线l1的距离为$\frac{9}{4}$.若$\overrightarrow{F{B}_{2}}$•$\overrightarrow{{A}_{1}{B}_{2}}$=1-2$\sqrt{3}$,则椭圆的标准方程是( )
| A. | $\frac{{x}^{2}}{4}$+y2=1 | B. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1 | C. | $\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{3}$+y2=1 |
2.若函数f(x)是定义在R上的偶函数,在(-∞,0)上对任意两个不相等的实数a,b总有$\frac{f(a)-f(b)}{a-b}$>0,且f(2)=0,则使xf(x)<0的x的取值范围是( )
| A. | -2<x<2 | B. | x>2或-2<x<0 | C. | -2<x<0 | D. | x<-2或x>2 |