题目内容
5．已知复数z满足zi=1-i，（i为虚数单位），则|z|=（ ）| A． | 1 | B． | 2 | C． | 3 | D． | $\sqrt{2}$ |
分析 根据复数的代数运算法则，求出复数z，再求它的模长即可．
解答 解：∵复数z满足zi=1-i，（i为虚数单位），
∴z=$\frac{1-i}{i}$=-i-1，
∴|z|=$\sqrt{{（-1）}^{2}{+（-1）}^{2}}$=$\sqrt{2}$．
故选：D．
点评 本题考查了复数的化简与运算问题，是基础题目．
练习册系列答案
孟建平错题本系列答案
超能学典应用题题卡系列答案
相关题目
15．设对任意实数x＞y＞0，若不等式x+2$\sqrt{xy}$＞ay恒成立，则实数a的取值范围为（ ）
| A． | （-∞，0） | B． | （-∞，0] | C． | （-∞，3） | D． | （-∞，3] |
16．阅读如图所示的程序框图，若运行该程序后输出的y的值为4，则输入的实数x的值为（ ）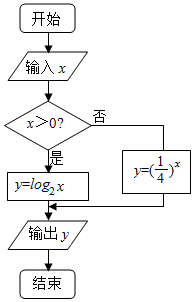
| A． | 4 | B． | 16 | C． | -1或16 | D． | -1或$\frac{1}{16}$ |
13．设F1，F2是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右两个焦点，若双曲线右支上存在一点P，使（$\overrightarrow{OP}$+$\overrightarrow{O{F}_{2}}$）•（$\overrightarrow{OP}$-$\overrightarrow{O{F}_{2}}$）=0（O为坐标原点），且|PF1|=$\sqrt{2}$|PF2|，则双曲线的离心率为（ ）
| A． | $\frac{\sqrt{3}+2}{2}$ | B． | $\sqrt{3}$+2 | C． | $\frac{\sqrt{3}+\sqrt{6}}{2}$ | D． | $\sqrt{3}$+$\sqrt{6}$ |
20．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点为F（c，0），过F且垂直于x轴的直线在第一象限内与双曲线、双曲线的渐近线的交点依次为A，B，若A为BF的中点，则双曲线的离心率为（ ）
| A． | $\frac{2\sqrt{3}}{3}$ | B． | $\sqrt{2}$ | C． | 2 | D． | 3 |
10．曲线y=x2与x=1及坐标轴围成的封闭区域为Ω1，不等式组$\left\{\begin{array}{l}{0≤x≤1}\\{0≤y≤1}\end{array}\right.$表示的平面区域为Ω2，在区域Ω2内随机取一点，则该点是取自于区域Ω1的概率是（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{2}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{2}{5}$ |
已知函数f（x）=2sin（ωx+φ）（ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$）的部分图象如图所示；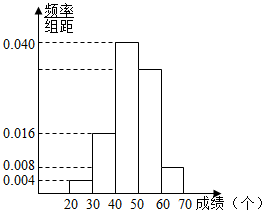
体育课上，李老师对初三 （1）班50名学生进行跳绳测试，现测得他们的成绩（单位：个）全部介于20与70之间，将这些成绩数据进行分组（第一组：（20，30]，第二组：（30，40]，…，第五组：（60，70]），并绘制成如图所示的频率分布直方图．