题目内容

16．阅读如图所示的程序框图，若运行该程序后输出的y的值为4，则输入的实数x的值为（　　）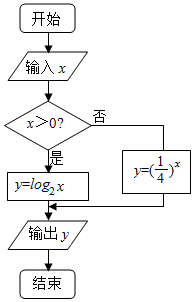
A．4B．16C．-1或16D．-1或$\frac{1}{16}$

分析 模拟执行程序得程序框图的功能是计算并输出y=$\left\{\begin{array}{l}{lo{g}_{2}x}&{x＞0}\\{（\frac{1}{4}）^{x}}&{x≤0}\end{array}\right.$ 的值，由题意，可得$\left\{\begin{array}{l}{x＞0}\\{lo{g}_{2}x=4}\end{array}\right.$，或$\left\{\begin{array}{l}{x≤0}\\{（\frac{1}{4}）^{x}=4}\end{array}\right.$，即可解得x的值．

解答 解：模拟执行程序，可得程序框图的功能是计算并输出y=$\left\{\begin{array}{l}{lo{g}_{2}x}&{x＞0}\\{（\frac{1}{4}）^{x}}&{x≤0}\end{array}\right.$ 的值，
由于运行该程序后输出的y的值为4，可得：$\left\{\begin{array}{l}{x＞0}\\{lo{g}_{2}x=4}\end{array}\right.$，或$\left\{\begin{array}{l}{x≤0}\\{（\frac{1}{4}）^{x}=4}\end{array}\right.$，
解得：x=16，或-1．
故选：C．

点评 本题考查解决程序框图的选择结构时，关键是判断出输入的值是否满足判断框中的条件，属于基础题．

练习册系列答案
相关题目
6．在数列{an}中，已知a1=4，an+1=3an-2n+1，n∈N+．
（1）设bn=an-n，求证：数列{bn}是等比数列；
（2）求数列{an}的前n项和Sn．
7．若双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$（a＞0，b＞0）的渐近线与圆C：${（x-1）^2}+{y^2}=\frac{1}{2}$相切，且圆C的圆心是双曲线的其中一个焦点，则双曲线的实轴长为$\sqrt{2}$．
4．已知圆C的参数方程为$\left\{\begin{array}{l}{x=4cosα}\\{y=4sinα}\end{array}\right.$（α为参数，0≤α＜2π），直线l的参数方程为$\left\{\begin{array}{l}{x=a-2t}\\{y=2\sqrt{3}t}\end{array}\right.$（t为参数）．
（Ⅰ）当a=0时，求直线l和圆C交点的直角坐标；
（Ⅱ）以坐标原点O为极点，x轴正半轴为极轴建立极坐标系，若直线l与圆C交于P、Q两点，若Q间的劣弧长为$\frac{8π}{3}$，求直线l的极坐标方程．
11．已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1（a＞0，b＞0）的两条渐近线的斜率之积为-2，焦距为6，则双曲线的方程为（　　）
A．$\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{24}$=1B．$\frac{x^2}{24}$-$\frac{y^2}{12}$=1C．$\frac{x^2}{3}$-$\frac{y^2}{6}$=1D．$\frac{x^2}{6}$-$\frac{y^2}{3}$=1
1．如图：抛物线y2=x与直线x=ty-1交于A，B两点，点B关于x轴的对称点为C，则直线AC在x轴上的截距（　　）
A．1B．$\frac{1}{2}$
C．$\frac{1}{4}$D．不是定值，与t的值相关
8．设双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的右焦点为F，点F到渐近线的距离为2a，则该双曲线的离心率等于（　　）
A．$\sqrt{2}$B．$\sqrt{3}$C．$\sqrt{5}$D．3
5．已知复数z满足zi=1-i，（i为虚数单位），则|z|=（　　）
A．1B．2C．3D．$\sqrt{2}$
6．在等比数列{an}中，a3，a15是方程x2-6x+8=0的根，则$\frac{{{a_1}{a_{17}}}}{a_9}$的值为（　　）
A．$2\sqrt{2}$B．4C．$±2\sqrt{2}$D．±4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网