题目内容
同时抛掷4枚均匀的硬币80次,设4枚硬币正好出现2枚正面向上,2枚反面向上的次数为ξ.
(Ⅰ)求抛掷4枚硬币,恰好2枚正面向上,2枚反面向上的概率;
(Ⅱ)求ξ的数学期望和方差.
(Ⅰ)求抛掷4枚硬币,恰好2枚正面向上,2枚反面向上的概率;
(Ⅱ)求ξ的数学期望和方差.
考点:离散型随机变量的期望与方差,离散型随机变量及其分布列
专题:概率与统计
分析:(Ⅰ)设“抛掷4枚硬币,恰好2枚正面向上,2枚反面向上”为事件A,抛掷4枚硬币的基本事件总数是24,其中事件A含
个基本事件,由此能求出掷4枚硬币,恰好2枚正面向上,2枚反面向上的概率.
(Ⅱ)由题意知ξ=0,1,2,3,…,80,ξ~B(80,
),由此能求出ξ的数学期望和方差.
| C | 2 4 |
(Ⅱ)由题意知ξ=0,1,2,3,…,80,ξ~B(80,
| 3 |
| 8 |
解答:
解:(Ⅰ)设“抛掷4枚硬币,恰好2枚正面向上,2枚反面向上”为事件A,
∵抛掷4枚硬币的基本事件总数是24,
其中事件A含
个基本事件,
∴P(A)=
=
,
∴掷4枚硬币,恰好2枚正面向上,2枚反面向上的概率是
.
(Ⅱ)由题意知ξ=0,1,2,3,…,80,
由(1)知抛掷4枚硬币,恰好2枚正面向上,两枚反面向上的概率是
,
又∵所抛掷的80次独立,
∴ξ~B(80,
),
∴Eξ=np=80×
=30,
Dξ=np(1-p)=80×
×(1-
)=
.
∵抛掷4枚硬币的基本事件总数是24,
其中事件A含
| C | 2 4 |
∴P(A)=
| ||
| 24 |
| 3 |
| 8 |
∴掷4枚硬币,恰好2枚正面向上,2枚反面向上的概率是
| 3 |
| 8 |
(Ⅱ)由题意知ξ=0,1,2,3,…,80,
由(1)知抛掷4枚硬币,恰好2枚正面向上,两枚反面向上的概率是
| 3 |
| 8 |
又∵所抛掷的80次独立,
∴ξ~B(80,
| 3 |
| 8 |
∴Eξ=np=80×
| 3 |
| 8 |
Dξ=np(1-p)=80×
| 3 |
| 8 |
| 3 |
| 8 |
| 75 |
| 4 |
点评:本题考查概率的求法,考查离散型随机变量的数学期望和方差的求法,解题时要认真审题,注意二项分布的合理运用.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案
相关题目
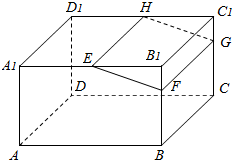 如图,在长方体ABCD-A1B1C1D1中,E、H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G
如图,在长方体ABCD-A1B1C1D1中,E、H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G