题目内容
5.设D为△ABC所在平面内一点$\overrightarrow{BC}$=3$\overrightarrow{CD}$,则( )| A. | $\overrightarrow{AD}$=$\frac{4}{3}$$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$ | B. | $\overrightarrow{AD}$=$\frac{4}{3}$$\overrightarrow{AB}$-$\frac{1}{3}$$\overrightarrow{AC}$ | C. | $\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$-$\frac{4}{3}$$\overrightarrow{AC}$ | D. | $\overrightarrow{AD}$=-$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{4}{3}$$\overrightarrow{AC}$ |
分析 $\overrightarrow{AD}=\overrightarrow{AC}+\overrightarrow{CD}$=$\overrightarrow{AC}$+$\frac{1}{3}\overrightarrow{BC}$=$\overrightarrow{AC}$+$\frac{1}{3}(\overrightarrow{BA}+\overrightarrow{AC})$=$\frac{4}{3}\overrightarrow{AC}$-$\frac{1}{3}\overrightarrow{AB}$.
解答 解:如图,$\overrightarrow{AD}=\overrightarrow{AC}+\overrightarrow{CD}$=$\overrightarrow{AC}$+$\frac{1}{3}\overrightarrow{BC}$=$\overrightarrow{AC}$+$\frac{1}{3}(\overrightarrow{BA}+\overrightarrow{AC})$
=$\frac{4}{3}\overrightarrow{AC}$-$\frac{1}{3}\overrightarrow{AB}$,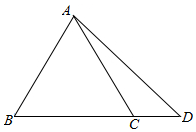
故选:D.
点评 本题考查向量的线性运算,属于中档题.

练习册系列答案
相关题目
13.椭圆$\left\{\begin{array}{l}{x=4cosθ}\\{y=3sinθ}\end{array}\right.$(θ为参数)的左焦点的坐标是( )
| A. | (-$\sqrt{7}$,0) | B. | (0,-$\sqrt{7}$) | C. | (-5,0) | D. | (-4,0) |
10.已知函数f(x)=$\left\{\begin{array}{l}{x+1,x≤0}\\{lgx,x>0}\end{array}\right.$,若函数y=|f(x)|-a有4个零点x1,x2,x3,x4,则x1+x2+x3+x4的取值范围是( )
| A. | (0,$\frac{81}{10}$] | B. | (0,$\frac{101}{10}$] | C. | (0,+∞) | D. | (2,$\frac{81}{10}$] |
17.已知函数函数$f(x)=\frac{1}{3}{x^3}+\frac{1-a}{2}{x^2}-ax-a$,其中a>0,若函数f(x)在区间(-2,0)内恰好有两个零点,则实数a的取值范围是( )
| A. | (0,3) | B. | (3,+∞) | C. | $(0,\frac{1}{3})$ | D. | $(\frac{1}{3},+∞)$ |