题目内容
9．
某单位有40名职工，现从中抽取5名职工，统计他们的体重，获得体重数据的茎叶图如图所示，则该样本的标准差为$\sqrt{62}$．
分析 先求出样本数据的平均数，再求出样本数据方差，由此能求出该样本的标准差．
解答 解：样本数据的平均数$\overline{x}$=$\frac{1}{5}（59+62+70+73+81）$=69，
样本数据方差S2=$\frac{1}{5}$[（59-69）2+（62-69）2+（70-69）2+（73-69）2+（81-69）2]=62，
∴该样本的标准差为S=$\sqrt{62}$．
故答案为：$\sqrt{62}$．
点评 本题考查样本数据标准差的求法，是基础题，解题时要认真审题，注意方差公式的合理运用．
练习册系列答案
步步高达标卷系列答案
相关题目
19．运行如图所示的程序，最后输出的结果是（ ）
| A． | 3 | B． | 1 | C． | c=3 | D． | c=1 |
17．根据如图所示的框图，当输入的x=3时，则输出的y为（ ）
| A． | 19 | B． | 10 | C． | 9 | D． | 0 |
4．F1，F2分别为椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1的左右焦点，P为椭圆上一动点，F2关于直线PF1的对称点为M，F1关于直线PF2的对称点为N，则当|MN|最大时，S${\;}_{△P{F}_{1}{F}_{2}}$为（ ）
| A． | 2 | B． | $\sqrt{2}$ | C． | $\frac{2\sqrt{3}}{3}$ | D． | $\frac{\sqrt{3}}{3}$ |
14．设i为虚数单位，复数z=i（5-i）在平面内对应的点的坐标为（ ）
| A． | （1，5） | B． | （l，-5） | C． | （-1，5） | D． | （-1，-5） |
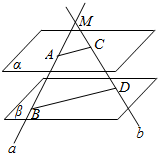如图所示，α∥β，M在α与β同侧，过M作直线a与b，a分别与α、β相交于A、B，b分别与α、β相交于C、D．