题目内容
7.已知函数f(x)=($\frac{1}{3}$)x+a的图象经过第二、三、四象限.(1)求实数a的取值范围;
(2)设g(a)=f(a)-f(a+1),求g(a)的取值范围.
分析 (1)直接由函数的图象平移结合图象求得a的取值范围;
(2)求出g(a),再由(1)中求得的a的范围得到g(a)的取值范围.
解答 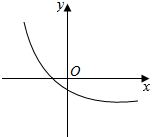 解:(1)如图,
解:(1)如图,
∵函数f(x)=($\frac{1}{3}$)x+a的图象经过第二、三、四象限,
∴a<-1;
(2)g(a)=f(a)-f(a+1)
=$(\frac{1}{3})^{a}+a-(\frac{1}{3})^{a+1}-a$=$(\frac{1}{3})^{a}(1-\frac{1}{3})=\frac{2}{3}•(\frac{1}{3})^{a}$.
∵a<-1,
∴$(\frac{1}{3})^{a}>3$,
则$\frac{2}{3}•(\frac{1}{3})^{a}>2$.
故g(a)的取值范围是(2,+∞).
点评 本题考查指数式的图象变换,考查了指数不等式的解法,是基础题.

练习册系列答案
相关题目
17.根据如图所示的框图,当输入的x=3时,则输出的y为( )


| A. | 19 | B. | 10 | C. | 9 | D. | 0 |
15.若f(x)=$\left\{\begin{array}{l}{lgx,}&{x>0}\\{x+{∫}_{0}^{a}3{t}^{2}dt,}&{x≤0}\end{array}\right.$,f(f(1))=1,则a的值是( )
| A. | -1 | B. | -2 | C. | 2 | D. | 1 |
2.已知直线l与直线2x-3y+4=0关于直线x=1对称,则直线l的方程为( )
| A. | 2x+3y-8=0 | B. | 3x-2y+1=0 | C. | x+2y-5=0 | D. | 3x+2y-7=0 |
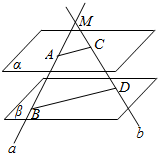 如图所示,α∥β,M在α与β同侧,过M作直线a与b,a分别与α、β相交于A、B,b分别与α、β相交于C、D.
如图所示,α∥β,M在α与β同侧,过M作直线a与b,a分别与α、β相交于A、B,b分别与α、β相交于C、D.