题目内容
已知函数f(x)=
是定义在(-1,1)上的函数.
(Ⅰ)判断函数f(x)的奇偶性(不需证明);
(Ⅱ)用定义法证明函数f(x)在(-1,1)上是增函数;
(Ⅲ)解不等式f(x-1)+f(x)<0.
| x |
| 1+x2 |
(Ⅰ)判断函数f(x)的奇偶性(不需证明);
(Ⅱ)用定义法证明函数f(x)在(-1,1)上是增函数;
(Ⅲ)解不等式f(x-1)+f(x)<0.
考点:奇偶性与单调性的综合,函数奇偶性的判断
专题:函数的性质及应用
分析:(Ⅰ)根据函数奇偶性的定义即可判断函数f(x)的奇偶性;
(Ⅱ)根据定义法证明函数f(x)在(-1,1)上是增函数;
(Ⅲ)根据奇偶性和单调性之间的关系将不等式进行转化即可.
(Ⅱ)根据定义法证明函数f(x)在(-1,1)上是增函数;
(Ⅲ)根据奇偶性和单调性之间的关系将不等式进行转化即可.
解答:
解:(Ⅰ)f(-x)=-
=-f(x),则f(x)为奇函数.
(Ⅱ)证明:对于任意的x1,x2∈(-1,1),且x1<x2,
,
∵-1<x1<x2<1,∴x1-x2<0,(1+
)(1+
)>0,
∴x1x2<1,∴1-x1x2>0.
∴f(x1)-f(x2)<0,即f(x1)<f(x2).
∴函数f(x)=
在(-1,1)上是增函数.…(7分)
(Ⅱ)由已知及(Ⅰ)知,f(x)是奇函数且在(-1,1)上递增,
…(11分)
∴不等式的解集为(0,
).…(12分)
| x |
| 1+x2 |
(Ⅱ)证明:对于任意的x1,x2∈(-1,1),且x1<x2,
|
∵-1<x1<x2<1,∴x1-x2<0,(1+
| x | 2 1 |
| x | 2 2 |
∴x1x2<1,∴1-x1x2>0.
∴f(x1)-f(x2)<0,即f(x1)<f(x2).
∴函数f(x)=
| x |
| 1+x2 |
(Ⅱ)由已知及(Ⅰ)知,f(x)是奇函数且在(-1,1)上递增,
|
∴不等式的解集为(0,
| 1 |
| 2 |
点评:本题主要考查函数奇偶性和单调性的判断和应用,利用定义法是解决本题的关键.

练习册系列答案
相关题目
已知某几何体的三视图如图所示,则该几何体的体积等于( )


A、
| ||
| B、32 | ||
C、
| ||
D、
|
下列函数中,既是奇函数又是减函数的是( )
A、y=
| ||
| B、y=-tanx | ||
C、y=
| ||
| D、y=-x3(-1<x≤1) |
已知tanα=2
,且α∈(-π,0),则sinα-
cosα的值是( )
| 2 |
| 2 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
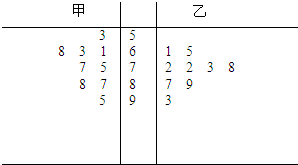 某班级甲乙两个小组各9名同学的期中考试数学成绩 (单位:分)的茎叶图如图
某班级甲乙两个小组各9名同学的期中考试数学成绩 (单位:分)的茎叶图如图