题目内容
某人在汽车站M的北偏西20°的方向上的A处(如图所示)，观察到C处有一辆汽车沿公路向M站行驶，公路的走向是M站的北偏东40°.开始时，汽车到A处的距离为31 km，汽车前进20 km后，到A处的距离缩短了10 km.问汽车还需行驶多远，才能到达汽车站M?
解：设汽车前进20 km后到达B处，在△ABC中，AC＝31，BC＝20，AB＝21，由余弦定理，得cosC＝
＝
，则sinC＝
.所以sin∠MAC＝sin
＝sin120°cosC－cos120°sinC＝
.在△MAC中，由正弦定理，得MC＝
＝35，从而有MB＝MC－BC＝15 km.
答：汽车还需行驶15 km，才能到达汽车站M.
练习册系列答案
相关题目
＝－
.
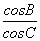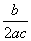，a＋c＝4，求△ABC的面积．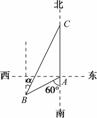
的图象，则φ＝________．
，求
的值．
，则直线l的斜率k的取值范围是______________．