题目内容
(1)若0<α<
,试比较α,sinα,tanα的大小;
(2)若0<α<β<
,试比较β-sinβ与α-sinα的大小.
| π |
| 2 |
(2)若0<α<β<
| π |
| 2 |
考点:利用导数研究函数的单调性
专题:综合题,导数的综合应用
分析:(1)画出单位圆,利用三角函数线及三角形、扇形面积公式可比较大小.
(2)构造函数f(x)=x-sinx,x∈(0,
),利用导数可判断单调性,由单调性可得结论;
(2)构造函数f(x)=x-sinx,x∈(0,
| π |
| 2 |
解答:
 解:(1)如图所示:sinα=MP,tanα=AT,
解:(1)如图所示:sinα=MP,tanα=AT,
S△OAP<S扇形POA<S△AOT,即
MP<
α<
AT,
∴
sinα<
α<
tanα,
∴sinα<α<tanα.
(2)令f(x)=x-sinx,x∈(0,
),
则f′(x)=1-cosx>0,
∴f(x)在(0,
)上单调递增,
又0<α<β<
,
∴f(α)<f(β),即α-sinα<β-sinβ.
 解:(1)如图所示:sinα=MP,tanα=AT,
解:(1)如图所示:sinα=MP,tanα=AT,S△OAP<S扇形POA<S△AOT,即
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴sinα<α<tanα.
(2)令f(x)=x-sinx,x∈(0,
| π |
| 2 |
则f′(x)=1-cosx>0,
∴f(x)在(0,
| π |
| 2 |
又0<α<β<
| π |
| 2 |
∴f(α)<f(β),即α-sinα<β-sinβ.
点评:该题考查三角函数线的应用,考查利用导数研究函数的单调性,考查学生解决问题的能力.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
已知i是虚数单位,则
=( )
| i2(-1+i) |
| 1+i |
| A、-1 | B、1 | C、-i | D、i |
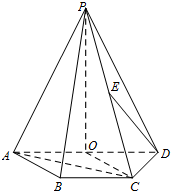 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,CD⊥平面PAD,BC∥AD,PA=PD,O,E分别为AD,PC的中点,PO=AD=2BC=2CD.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,CD⊥平面PAD,BC∥AD,PA=PD,O,E分别为AD,PC的中点,PO=AD=2BC=2CD.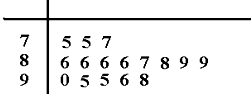 某统计部门用“10分制”调查一社区人们对物业管理的“满意度”.现从调查人群中随机抽取16名,以下茎叶图记录了他们的“满意度”分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):
某统计部门用“10分制”调查一社区人们对物业管理的“满意度”.现从调查人群中随机抽取16名,以下茎叶图记录了他们的“满意度”分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):