题目内容
18.若(a+1)2>(a+1)3(a≠-1),则实数a的取值范围是a<0且a≠-1.分析 原不等式等价于a(a+1)2<0,穿根法可得.
解答 解:原不等式等价于(a+1)2-(a+1)3>0,
分解因式可得(a+1)2(1-a-1)>0,
等价于a(a+1)2<0,
解得a<0且a≠-1
故答案为:a<0且a≠-1.
点评 本题考查高次不等式的解法,分解因式是解决问题的关键,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.下列命题中的假命题是( )
| A. | ?x∈R,ex>0 | B. | ?x∈R,lnx=0 | C. | ?x∈R,(x-1)2≥0 | D. | ?x∈R,x2+1=0 |
7.下列条件,能使sinα+cossα>1成立的是( )
| A. | 0<α<π | B. | 0<α<$\frac{3π}{2}$ | C. | 0<α<$\frac{π}{2}$ | D. | $\frac{π}{4}$≤α≤$\frac{π}{2}$ |
8.一个几何体的三视图如图所示,则这个几何体的体积为( )
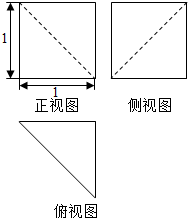

| A. | $\frac{5}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
 在六棱柱ABCDEFA1B1C1D1E1F1中.
在六棱柱ABCDEFA1B1C1D1E1F1中.