题目内容
13.已知函数f(x)=$\frac{{2}^{x}+a}{{2}^{x}+1}$为奇函数.(1)求实数a的值;
(2)试判断函数的单调性并加以证明;
(3)对任意的x∈R,不等式f(x)<m恒成立,求实数m的取值范围.
分析 (1)解f(0)=0可得a值;
(2)由单调性的定义可得;
(3)由(1)(2)可得函数f(x)为增函数,当x趋向于正无穷大时,f(x)趋向于1,可得m≥1.
解答 解:(1)由函数为奇函数可得f(0)=$\frac{1+a}{2}$=0,解得a=-1;
(2)由(1)可得f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$=$\frac{{2}^{x}+1-2}{{2}^{x}+1}$=1-$\frac{2}{{2}^{x}+1}$,
可得函数在R上单调递增,下面证明:
任取实数x1<x2,则f(x1)-f(x2)
=$\frac{2}{{2}^{{x}_{2}}+1}$-$\frac{2}{{2}^{{x}_{1}}+1}$=$\frac{2({2}^{{x}_{1}}-{2}^{{x}_{2}})}{({2}^{{x}_{1}}+1)({2}^{{x}_{2}}+1)}$<0,
∴函数f(x)=$\frac{{2}^{x}+a}{{2}^{x}+1}$R上的增函数;
(3)∵函数f(x)为增函数,当x趋向于正无穷大时,f(x)趋向于1,
要使不等式f(x)<m恒成立,则需m≥1
点评 本题考查函数的奇偶性和单调性以及恒成立问题,属中档题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
8.设函数f(x)=$\sqrt{2}$sin(ωx+φ+$\frac{π}{4}$)(ω>0,|φ|<$\frac{π}{2}$)的最小正周期为π,且f(-x)=f(x),则( )
| A. | f(x)在(0,$\frac{π}{2}$)单调递减 | B. | f(x)在($\frac{π}{4}$,$\frac{3π}{4}$)单调递减 | ||
| C. | f(x)在(0,$\frac{π}{2}$)单调递增 | D. | f(x)在($\frac{π}{4}$,$\frac{3π}{4}$)单调递增 |
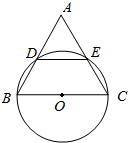 如图,以⊙O的直径BC为一边作等边△ABC,AB、AC交⊙O于点DE,求证:BD=DE=EC.
如图,以⊙O的直径BC为一边作等边△ABC,AB、AC交⊙O于点DE,求证:BD=DE=EC.