题目内容
19.已知圆x2+y2+2x-2y-4=0截直线x+y+2=0所得弦的长度是( )| A. | 2 | B. | .4 | C. | .6 | D. | .8 |
分析 直接根据弦长公式L=$2\sqrt{{r}^{2}-{d}^{2}}$求解即可.d圆心到直线的距离.
解答 解:圆x2+y2+2x-2y-4=0,
可得圆的标准方程为(x+1)2+(y-1)=6.
圆心为(-1,1),r=$\sqrt{6}$.
圆心到直线的距离d=$\frac{2}{\sqrt{2}}=\sqrt{2}$.
那么:弦长L=$2\sqrt{{r}^{2}-{d}^{2}}$=4.
故选:B.
点评 本题主要考查直线和圆的位置关系,弦长的公式运用,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.执行如图所示的程序框图,输出的结果是( )


| A. | 13 | B. | 11 | C. | 9 | D. | 7 |
10. 如图,一个正六角星薄片(其对称轴与水平面垂直)匀速地升长水面,直到全部露出水面为止,记时刻t薄片露出水面部分的图形面积为S(t)(S(0)=0),则导函数y=S'(x)的图象大致为( )
如图,一个正六角星薄片(其对称轴与水平面垂直)匀速地升长水面,直到全部露出水面为止,记时刻t薄片露出水面部分的图形面积为S(t)(S(0)=0),则导函数y=S'(x)的图象大致为( )
 如图,一个正六角星薄片(其对称轴与水平面垂直)匀速地升长水面,直到全部露出水面为止,记时刻t薄片露出水面部分的图形面积为S(t)(S(0)=0),则导函数y=S'(x)的图象大致为( )
如图,一个正六角星薄片(其对称轴与水平面垂直)匀速地升长水面,直到全部露出水面为止,记时刻t薄片露出水面部分的图形面积为S(t)(S(0)=0),则导函数y=S'(x)的图象大致为( )| A. | 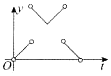 | B. | 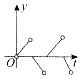 | C. | 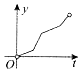 | D. | 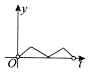 |
14.将3个不同的小球放入4个不同的盒子中,则不同的放法种数有( )
| A. | 12 | B. | 14 | C. | 64 | D. | 81 |
9.在△ABC中,∠A=60°,b=1,S△ABC=$\sqrt{3}$,则$\frac{a-2b+c}{sinA-2sinB+sinC}$的值等于( )
| A. | $\frac{{2\sqrt{39}}}{3}$ | B. | $\frac{26}{3}\sqrt{3}$ | C. | $\frac{8}{3}\sqrt{3}$ | D. | $2\sqrt{3}$ |