题目内容
7.已知$cos({α+β})=\frac{2}{3},cos({α-β})=\frac{1}{3}$,则tanα•tanβ=-$\frac{1}{3}$.分析 利用两角和与差的余弦函数公式化简已知两等式,再利用同角三角函数间的基本关系化简,即可求出tanα•tanβ的值.
解答 解:∵cos(α+β)=cosαcosβ-sinαsinβ=$\frac{2}{3}$,
cos(α-β)=cosαcosβ+sinαsinβ=$\frac{1}{3}$,
∴$\frac{cos(α+β)}{cos(α-β)}$=$\frac{cosαcosβ-sinαsinβ}{cosαcosβ+sinαsinβ}$=$\frac{1-tanαtanβ}{1+tanαtanβ}$=2,
即1-tanαtanβ=2+2tanαtanβ,
整理得:tanαtanβ=-$\frac{1}{3}$.
故答案为:-$\frac{1}{3}$.
点评 此题考查了两角和与差的余弦函数公式,以及同角三角函数间的基本关系,熟练掌握公式是解本题的关键,属于基础题.

练习册系列答案
相关题目
2.为了解某班学生喜爱打篮球是否与性别有关,对该班50名学生进行了问卷调查,得到如图的2×2列联表.
则至少有( )的把握认为喜爱打篮球与性别有关.
附参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
附参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2>k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.789 | 10.828 |
| A. | 95% | B. | 99% | C. | 99.5% | D. | 99.9% |
12.已知集合A={x|x≥3或x≤-1},B={x|=-2≤x≤2},则A?B=( )
| A. | [-2,-1] | B. | [-1,2) | C. | [-1,1] | D. | [1,2) |
19.已知圆x2+y2+2x-2y-4=0截直线x+y+2=0所得弦的长度是( )
| A. | 2 | B. | .4 | C. | .6 | D. | .8 |
16.设f(x)是可导函数,且$\lim_{△x→0}\frac{{f({x_0})-f({{x_0}+2△x})}}{△x}=2$,则f'(x0)=( )
| A. | $\frac{1}{2}$ | B. | -1 | C. | 0 | D. | -2 |
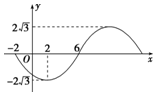 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示.
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示.