题目内容
已知全集U=R,函数f(x)=log3(x2+x-2)的定义域为A,关于x的不等式|x-2|>a的解集为B.
(Ⅰ)若命题:x∈B是命题x∈A成立的充分不必要条件,求实数a的取值范围;
(Ⅱ)若A∪B=U,求实数a的取值范围.
(Ⅰ)若命题:x∈B是命题x∈A成立的充分不必要条件,求实数a的取值范围;
(Ⅱ)若A∪B=U,求实数a的取值范围.
考点:函数与方程的综合运用,必要条件、充分条件与充要条件的判断,函数的定义域及其求法,绝对值不等式的解法
专题:函数的性质及应用
分析:(Ⅰ)由x2+x-2>0 可得 x<-2,或 x>1,可得A,解绝对值不等式求出B,通过x∈B是命题x∈A成立的充分不必要条件,推出B?A,列出不等式求解即可.
(Ⅱ)若A∪B=U,由(Ⅰ)列出不等式,从而求得实数a的取值范围.
(Ⅱ)若A∪B=U,由(Ⅰ)列出不等式,从而求得实数a的取值范围.
解答:
解:(Ⅰ)要使函数f(x)=log3(x2+x-2)有意义,必有x2+x-2>0 可得 x<-2,或 x>1,
所以函数的定义域A={x|x<-2,或 x>1},
关于x的不等式|x-2|>a的解集为B={x|x<2-a或x>2+a}.
命题:x∈B是命题x∈A成立的充分不必要条件,可得B?A,即
,解得a≥4.
实数a的取值范围:[4,+∞).
(Ⅱ)若A∪B=U,则2-a>2或2+a<-2,解得:a<-4,
故实数a的取值范围为(-∞,-4).
所以函数的定义域A={x|x<-2,或 x>1},
关于x的不等式|x-2|>a的解集为B={x|x<2-a或x>2+a}.
命题:x∈B是命题x∈A成立的充分不必要条件,可得B?A,即
|
实数a的取值范围:[4,+∞).
(Ⅱ)若A∪B=U,则2-a>2或2+a<-2,解得:a<-4,
故实数a的取值范围为(-∞,-4).
点评:本题主要考查绝对值不等式、对数不等式的解法,集合关系中参数的取值范围问题,函数与方程的应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
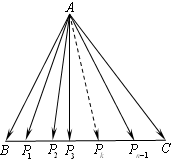 若在边长为1的正三角形△ABC的边BC上有n(n∈N*,n≥2)等分点,沿向量
若在边长为1的正三角形△ABC的边BC上有n(n∈N*,n≥2)等分点,沿向量| BC |
| AB |
| AP1 |
| AP1 |
| AP2 |
| APn-1 |
| AC |
A、
| ||
B、
| ||
C、
| ||
D、
|

 已知y=f(x)是定义在(-∞,0)∪(0,+∞)上的奇函数,当x>0时,f(x)=log2x,
已知y=f(x)是定义在(-∞,0)∪(0,+∞)上的奇函数,当x>0时,f(x)=log2x,