题目内容
已知△ABC中，|AC|=|BC|=2，∠ACB=90°，M为BC的中点，D为以AC为直径的圆上一动点，E为直径AC上的动点，则
•
-
•
的取值范围是 ．
| AM |
| AE |
| AM |
| DE |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：建立坐标系，明确A，M，D的坐标，以及向量
，
的坐标，利用向量的数量积得到关于α的解析式求范围．
| AM |
| AD |
解答：
解：由题意，建立如图所示的直角坐标系，则A（-1，0），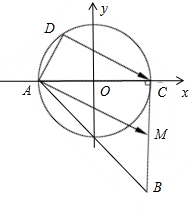
M（1，-1），设D（cosα，sinα）．
∴
=（2，-1），
=（cosα+1，sinα）．
∴
•
-
•
=
•
=2cosα+2-sinα=2+
sin（θ-α），其中tanθ=2．
∵sin（θ-α）∈[-1，1]，
∴2+
sin（θ-α）∈[2-
，2+
]，
∴
•
-
•
的取值范围是[2-
，2+
]．
故答案为：[2-
，2+
]．
M（1，-1），设D（cosα，sinα）．∴
| AM |
| AD |
∴
| AM |
| AE |
| AM |
| DE |
| AM |
| AD |
| 5 |
∵sin（θ-α）∈[-1，1]，
∴2+
| 5 |
| 5 |
| 5 |
∴
| AM |
| AE |
| AM |
| DE |
| 5 |
| 5 |
故答案为：[2-
| 5 |
| 5 |
点评：本题考查平面向量的数量积的运用，涉及三角函数的值域，关键是建系通过向量的数量积得到关于α的三角函数解析式，利用正弦函数的有界性解决问题，属中档题．
练习册系列答案
相关题目
已知函数f（x）=2（x-a）（x-b）（其中a＞b）的图象如右图，则函数g（x）=ax+b的图象一定不过第下列终边相同的是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、（2k+1）π，（4k+1）π，k∈Z |
已知图1、图2分别表示A、B两城市某月1日至6日当天最低气温的数据折线图（其中横轴n表示日期，纵轴x表示气温），记A、B两城市这6天的最低气温平均数分别为
和
，标准差分别为sA和sB，则它们的大小关系是（ ）
. |
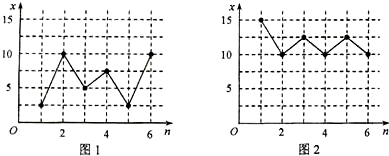
| xA |
. |
| xB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|