题目内容
17．在△ABC中，角A、B、C所对边分别为a、b、c，若a2+b2=4a+6b-13，sinC=2sinA，则cosC的值为（ ）| A． | -$\frac{1}{4}$ | B． | $\frac{1}{4}$ | C． | $\frac{7}{8}$ | D． | $\frac{11}{16}$ |
分析 利用配方法，求出a，b，利用正弦定理，求出c，利用余弦定理，求出cosC的值．
解答 解：∵a2+b2=4a+6b-13，
∴（a-2）2+（b-3）2=0，
∴a=2，b=3，
∵sinC=2sinA，
∴c=2a=4，
∴cosC=$\frac{4+9-16}{2×2×3}$=-$\frac{1}{4}$．
故选：A．
点评 本题考查正弦、余弦定理，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
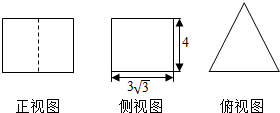若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如图所示，则这个棱柱的表面积为$72+18\sqrt{3}$．则这个棱柱体积为36$\sqrt{3}$．