题目内容
9.求值:(1)${0.027^{-\frac{1}{3}}}-{(-\frac{1}{7})^{-2}}+{256^{\frac{3}{4}}}-{3^{-1}}$+1
(2)log43•log92+log2$\root{4}{64}$.
分析 根据指数幂和对数的运算性质计算即可.
解答 解:(1).${0.027^{-\frac{1}{3}}}-{(-\frac{1}{7})^{-2}}+{256^{\frac{3}{4}}}-{3^{-1}}+1$
=${({0.3^3})^{-\frac{1}{3}}}-{(-7)^2}+{({4^4})^{\frac{3}{4}}}-\frac{1}{3}+1$,
=19
(2)$原式=\frac{lg3}{lg4}•\frac{lg2}{lg9}+{log_2}{2^{\frac{6}{4}}}$=$\frac{1}{4}+\frac{6}{4}$=$\frac{7}{4}$
点评 本题考查了指数幂和对数的运算性质,属于基础题.

练习册系列答案
相关题目
20.给出下列四个命题:
①若平面α∥β,直线a?α,直线b?β,则a∥b
②若直线a∥b,a∥α,则b∥α
③若平面α∥β,直线a?α,则a∥β
④若直线a∥α,a∥β,则α∥β
其中正确命题有( )
①若平面α∥β,直线a?α,直线b?β,则a∥b
②若直线a∥b,a∥α,则b∥α
③若平面α∥β,直线a?α,则a∥β
④若直线a∥α,a∥β,则α∥β
其中正确命题有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.在△ABC中,角A、B、C所对边分别为a、b、c,若a2+b2=4a+6b-13,sinC=2sinA,则cosC的值为( )
| A. | -$\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{7}{8}$ | D. | $\frac{11}{16}$ |
17.已知函数f(x)=-x2+ex-1(x≤1)与g(x)=ln(-x+a)的图象上存关于直线y=x-1对称的点,则a的取值范围是( )
| A. | (-∞,-2] | B. | [2,+∞) | C. | (-∞,2] | D. | [1,+∞) |
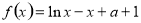 .
.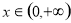 使得
使得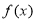 ≥0成立,求
≥0成立,求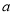 的范围;
的范围;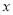 >1时,在(1)的条件下,
>1时,在(1)的条件下,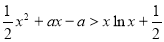 成立.
成立.