题目内容
9.已知函数f(x)=3x,x∈[-1,1],函数g(x)=[f(x)]2-2af(x)+3.(Ⅰ)当a=0时,求函数g(x)的值域;
(Ⅱ)若函数g(x)的最小值为h(a),求h(a)的表达式;
(Ⅲ)是否存在实数m,n同时满足下列两个条件:①m>n>3;②当h(a)的定义域为[n,m]时,值域为[n2,m2]?若存在,求出m,n的值;若不存在,请说明理由.
分析 (Ⅰ)设t=3x,则φ(t)=t2-2at+3=(t-a)2+3-a2,φ(t)的对称轴为t=a,当a=0时,即可求出g(x)的值域;
(Ⅱ)由函数φ(t)的对称轴为t=a,分类讨论当a<$\frac{1}{3}$时,当$\frac{1}{3}≤a≤3$时,当a>3时,求出最小值,则h(a)的表达式可求;
(Ⅲ)假设满足题意的m,n存在,函数h(a)在(3,+∞)上是减函数,求出h(a)的定义域,值域,然后列出不等式组,求解与已知矛盾,即可得到结论.
解答 解:(Ⅰ)∵函数f(x)=3x,x∈[-1,1],∴${3}^{x}∈[\frac{1}{3},3]$,设t=3x,$t∈[\frac{1}{3},3]$,
则φ(t)=t2-2at+3=(t-a)2+3-a2,对称轴为t=a.
当a=0时,φ(t)=t2+3,$t∈[\frac{1}{3},3]$,∴φ(t)∈[$\frac{28}{9}$,12],
∴函数g(x)的值域是:[$\frac{28}{9}$,12];
(Ⅱ)∵函数φ(t)的对称轴为t=a,
当a<$\frac{1}{3}$时,ymin=h(a)=φ($\frac{1}{3}$)=$\frac{28}{9}-\frac{2a}{3}$;
当$\frac{1}{3}≤a≤3$时,ymin=h(a)=φ(a)=3-a2;
当a>3时,ymin=h(a)=φ(3)=12-6a.
故$h(a)=\left\{\begin{array}{l}\frac{28}{9}-\frac{2a}{3}(a<\frac{1}{3})\\ 3-{a^2}(\frac{1}{3}≤a≤3)\\ \\ 12-6a(a>3)\end{array}\right.$,
(Ⅲ)假设满足题意的m,n存在,∵m>n>3,∴h(a)=12-6a,
∴函数h(a)在(3,+∞)上是减函数.
又∵h(a)的定义域为[n,m],值域为[n2,m2],
∴$\left\{\begin{array}{l}12-6m={n^2}\\ 12-6n={m^2}\end{array}\right.$,两式相减得6(m-n)=(m-n)•(m+n),
又∵m>n>3,∴m-n≠0,∴m+n=6,与m>n>3矛盾.
∴满足题意的m,n不存在.
点评 本题主要考查二次函数的值域问题,二次函数在特定区间上的值域问题一般结合图象和单调性处理,是中档题.

| A. | e2f(-15)<f(-6),e2f(-11)<f(-20) | B. | e2f(-15)>f(-6),e2f(-11)>f(-20) | ||
| C. | e2f(-15)<f(-6),e2f(-11)>f(-20) | D. | e2f(-15)>f(-6),e2f(-11)<f(-20) |
| A. | 5π | B. | 7π | C. | 9π | D. | 11π |
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
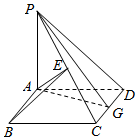 如图,ABCD是边长为a的正方形,PA⊥平面ABCD.
如图,ABCD是边长为a的正方形,PA⊥平面ABCD.