题目内容
平面向量中从集合A到A的映射f由f(x)=x-2(x•
)•
确定,其中
为常向量,若映射f满足f(x)•f(y)=x•y,对x,y∈A恒成立,则|
|=( )
| a |
| a |
| a |
| a |
| A、1 | ||
| B、2 | ||
C、
| ||
| D、2 |
考点:映射
专题:函数的性质及应用
分析:通过赋值列出关于向量的方程,通过向量的运算法则化简方程,得到
满足的条件.
| a |
解答:
解:令
=
,则则f(
)•f(
)=
•
=[
-2(
•
)•
]2=
2-4(
•
)2+4[(
•
)
]2,
即-4(
•
)2+4[(
•
)
]2=0,
∴(
•
)2(
2-1)=0
∴(
2-1)=0,
∴|
|=1,
故选:A.
| y |
| x |
| x |
| x |
| x |
| x |
| x |
| x |
| a |
| a |
| x |
| x |
| a |
| x |
| a |
| a |
即-4(
| x |
| a |
| x |
| a |
| a |
∴(
| x |
| a |
| a |
∴(
| a |
∴|
| a |
故选:A.
点评:本题以映射为载体考查向量的运算法则及向量的运算律,难度不大,属于基础题.

练习册系列答案
相关题目
定义运算
=
,称
=
为将点(x,y)映到点(x′,y′)的一次变换.若
=
把直线y=x上的各点映到这点本身,而把直线y=3x上的各点映到这点关于原点对称的点.则p,q的值分别是( )
|
|
|
|
|
|
|
|
| A、p=1,q=1 |
| B、p=3,q=1 |
| C、p=3,q=3 |
| D、p=3,q=-2 |
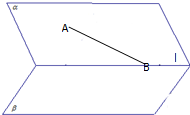 如图,二面角α-l-β中,点A∈β,点B∈l,直线AB与平面α所成的角为30°,直线AB与l夹角为45°,则二面角α-k-β的平面角的正弦值为( )
如图,二面角α-l-β中,点A∈β,点B∈l,直线AB与平面α所成的角为30°,直线AB与l夹角为45°,则二面角α-k-β的平面角的正弦值为( )